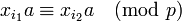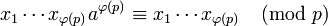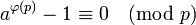Вычисление мультипликативных обратных элементов по заданному модулю
Рассмотрим вопрос о мультипликативных обратных элементов по заданному модулю в фактор-кольце 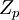 .
.
Рассмотрим два способа вычисления обратных мультипликативных элементов. Первый способ основан на рассмотренном выше алгоритме Евклида, второй – на теореме Эйлера.
Первый способ
Второй способ
Напомним теорему Эйлера.
Определение
Функция Эйлера 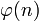 — это количество чисел от
— это количество чисел от 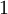 до
до  , взаимно простых с
, взаимно простых с  .
.
Т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с  равен единице.
равен единице.
Tеоремa Эйлера
Если  и
и  взаимно просты, то
взаимно просты, то 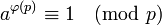 , где
, где 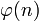 - функция Эйлера.
- функция Эйлера.
Доказательство теоремы достаточно простое, возможны различные варианты. Приведем здесь теоретико-числовое доказательство.
Доказательство.
Пусть 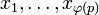 — все различные натуральные числа, меньшие
— все различные натуральные числа, меньшие  и взаимно простые с ним.
и взаимно простые с ним.
Рассмотрим все возможные произведения 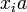 для всех
для всех 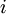 от
от 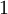 до
до 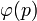 .
.
Поскольку  взаимно просто с
взаимно просто с  и
и 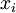 взаимно просто с
взаимно просто с  , то и
, то и 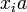 также взаимно просто с
также взаимно просто с  , то есть
, то есть 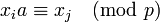 для некоторого
для некоторого 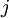 .
.
Отметим, что все остатки 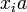 при делении на
при делении на  различны. Действительно, пусть это не так, то существуют такие
различны. Действительно, пусть это не так, то существуют такие 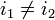 , что
, что
или
-
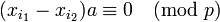 .
.
Так как  взаимно просто с
взаимно просто с  , то последнее равенство равносильно тому, что
, то последнее равенство равносильно тому, что
-
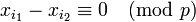 или
или 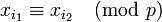 .
.
Это противоречит тому, что числа 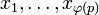 попарно различны по модулю
попарно различны по модулю  .
.
Перемножим все сравнения вида 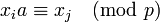 . Получим:
. Получим:
или
-
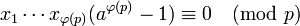 .
.
Так как число 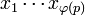 взаимно просто с
взаимно просто с  , то последнее сравнение равносильно тому, что
, то последнее сравнение равносильно тому, что
или
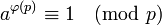 .
.
В частном случае, когда  простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Малая теорема Ферма
Если  - простое число и
- простое число и  - произвольное целое число, не делящееся на
- произвольное целое число, не делящееся на  , то
, то 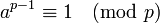 .
.