Свёртка (цифровая обработка сигналов)

Свёртка (англ. Convolution) — это базовая операция в задачах цифровой обработки сигналов. В дискретном случае различают два вида сверток: линейную и циклическую.

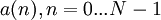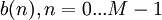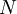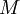Пусть имеется два дискретных сигнала $a(n), n=0...N-1$ и $b(n), n=0...M-1$. В общем случае $N$ и $M$ отличаются.

Линейная свёртка

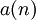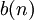Линейной сверткой сигналов $a(n)$ и $b(n)$ называется дискретный сигнал вида: $s(n)=\sum_{m=0}^{n}a(m)b(n-m), n=0...(N+M-2)$

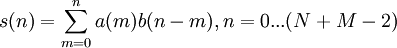
Для вычисления линейной свертки сигналы a(n)и b(n)сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что a(n)=0 при n<0 и n>N, и b(n)=0 при n<0 и n>M.

Циклическая свёртка

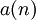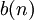В циклической свертке предполагается, что дискретные сигналы $a(n)$ и $b(n)$ – периодические с одинаковым периодом N отсчетов. Тогда циклической сверткой сигналов a(n) и b(n) называется сигнал вида: s(n)=∑_(m=0)^(N-1)▒〖a(m)∙b(n-m)〗, n=0…N-1 Результат циклической свертки также имеет длину N отсчетов.

Вычисление линейной свертки через циклическую

Используя циклическую свертку можно рассчитать линейную свертку двух сигналов. Для этого необходимо каждый из сигналов a(n)и b(n) длительностью M и N отсчетов соответственно дополнить нулями до длины M+N-1. Вычисление линейной свертки через циклическую кажется нерациональным, однако на практике чаще бывает удобно вычислять именно циклическую свертку, благодаря так называемой теореме о свертке. Cуть теоремы о свертке: спектр циклической свертки есть произведение спектров сворачиваемых сигналов: S(k)=A(k)*B(k), где A(k) и B(k) - спектры сворачиваемых сигналов, S(k) - спектр циклической свертки двух сигналов. Где спектр есть ни что иное как Дискретное преобразование Фурье (ДПФ), для реализации которого можно использовать быстрые алгоритмы БПФ

Применение

• Линейная свертка используется для расчета FIR-фильтров в цифровой обработке сигналов.
• Циклическую свертку используют для вычисления линейной свертки в том случае, если теорема о свертке дает хороший результат.