Схема коррекции ошибок Rajendra S. Katti
Введение
Метод, описанный автором, основан на использовании избыточной системы остаточных классов. Недостатки представления чисел в такой системе с целью коррекции ошибок при вычислениях покажем на примере.
Пусть избыточная СОК определяется следующими модулями 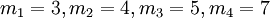 , а динамический диапазон определяется
, а динамический диапазон определяется 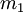 и
и 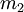 и соответственно равен
и соответственно равен  , а модули
, а модули 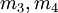 являются дополнительными и необходимы для проверки на ошибки.
являются дополнительными и необходимы для проверки на ошибки.
Натуральное число из динамического диапазона может быть восстановлено по любым трём из четырёх остатков по представленным модулям. Например, число 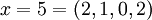 может быть представлено как
может быть представлено как 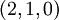 в системе модулей
в системе модулей 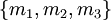 или
или 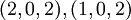 в системах
в системах 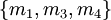 и
и 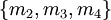 соответственно. Поэтому, если одна цифра отбрасывается в представлении
соответственно. Поэтому, если одна цифра отбрасывается в представлении 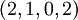 , правильный результат восстановления будет получен тогда и только тогда, когда отбрасываемая цифра ошибочна. Таким образом, обнаружение ошибок и коррекция выполняется следующим образом:
, правильный результат восстановления будет получен тогда и только тогда, когда отбрасываемая цифра ошибочна. Таким образом, обнаружение ошибок и коррекция выполняется следующим образом:
- Если число лежит вне динамического диапазона - произошла ошибка.
- Остатки отбрасываются по одному и если в результате одного из отбрасываний полученное число лежит в динамическом диапазоне, то отброшенный остаток является ошибочным.
- Корректное значение остатка получается расширением полученного на шаге 2 множества модулей, остатки по которым не содержат ошибок.
Такой подход требует много времени и вычислительных ресурсов. Ниже будет предложена новая схема обнаружения и коррекции ошибок на основе СОК.
Модули, имеющие общие делители
Каждый набор остатков необязательно соответствует числу из динамического диапазона, если модули не являются попарно взаимно простыми. Легко показать, что такое соответствие есть тогда и только тогда, когда
-
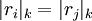 ,
,
выполняется для любых 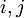 , где
, где 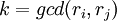 . Таким образом, ошибочный разряд может быть найден выполнением только простой операции вычисления остатка.
. Таким образом, ошибочный разряд может быть найден выполнением только простой операции вычисления остатка.
Приведём пример, демонстрирующий, как можно проверить набор остатков на наличие ошибок. Проверим набор 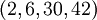 в системе модулей
в системе модулей 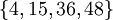 . Наибольшие общие делители всевозможных пар модулей соответственно равны:
. Наибольшие общие делители всевозможных пар модулей соответственно равны: 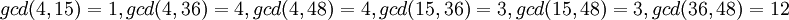 .
Используя описанное выше соотношение для проверки, получаем:
.
Используя описанное выше соотношение для проверки, получаем: 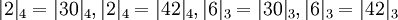 и
и 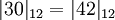 . То есть ошибок нет и число может быть восстановлено с использованием китайской теоремы об остатках (КТО) для модулей, имеющих нетривиальные общие делители.
. То есть ошибок нет и число может быть восстановлено с использованием китайской теоремы об остатках (КТО) для модулей, имеющих нетривиальные общие делители.
КТО для системы модулей, не взаимно простых попарно. Пусть есть представление 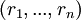 натурального числа
натурального числа  , определяемое системой модулей
, определяемое системой модулей 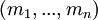 . Тогда
. Тогда
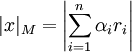 ,
,
где 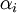 - число, такое что
- число, такое что 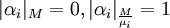 ,
где
,
где 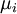 - числа, такие что
- числа, такие что 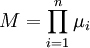 ,
, 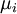 делит
делит 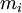 и
и 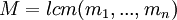 . Если для некоторого
. Если для некоторого 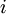 такое
такое 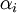 не существует, то соответствующее слагаемое в сумме опускается.
не существует, то соответствующее слагаемое в сумме опускается.
Операции над числами остаются корректными и в системе не взаимно простых модулей.