Песочница

Количество операций необходимых для вычисления воздействия FIR-фильтра

Пусть задан FIR-фильтр длины M и большая последовательность данных длины K. В этом случае можно разбить последовательность на несколько отрезков длины L и выполнить свертку по методу Overlap-Add или Overlap-Save. При этом метод выполнения свертки оказывается не важен. И количество операций будет пропорционально (K/L)*OPER - где OPER - оличество операций для метода, которым мы делаем линейную свертку.

Количество операций необходимых для вычисления линейной свертки

Пусть задан фильтр длины M и последовательность L и битность входных данных B.

Свертка по обычной формуле

По опеределению свертка вычисляется по формуле: 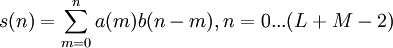$s(n)=\sum_{m=0}^{n}a(m)b(n-m), n=0...(L+M-2)$

Для выполнения свертки в этом случае потребуется M*L операций умножения размерности B-бит и (M-1)*L операций сложения размерности 2*B-бит.

Пример

M = 1024 L = 1024 B = 8 бит

• Количество операций 16-битного сложения: 1047552
• Количество операций 8-битного умножения: 1048576

Свертка через БПФ по тригонометрическому базису

1. Количество операций требующихся для вычисления одного прямого БПФ длины 2^N составляет (2^N)*N операций комплексного умножения и (2^N)*N операций комплексного сложения. Каждая операция комплексного умножения/сложения на прямом БПФ требует две операции обычного умножения/сложения.
2. Количество операций требующихся для вычисления одного обратного БПФ длины 2^N составляется (2^N)*N операций комплексного умножения и (2^N)*N операций комплексного сложения. При этом поскольку на обратном преобразовании мнимая часть у нас не нулевая, то комплексное умножение требует 4 целочисленных умножения и 2 целочисленных сложения. Однако если на входе были только целочисленные значения, то на выходе мнимая часть нас не интересует. Поэтому требуется только две операции целочисленного умножения и одна целочисленного сложения (требуется уточнить).
3. Вычисления произведения сверток длины (M+L-1) требует (M+L-1) комплексных умножения что равноценно 4*(M+L-1) целочисленных умножения и 2*(M+L-1) целочисленных сложения.