Сравнение разных методов сложения по модулю 2^n-1

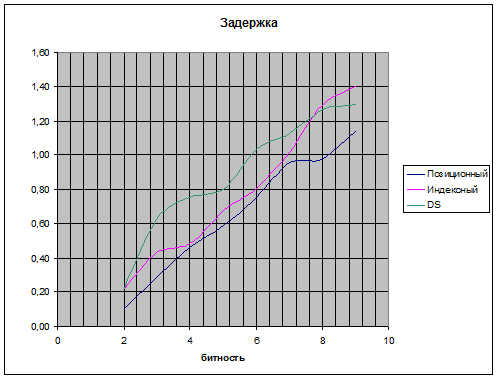
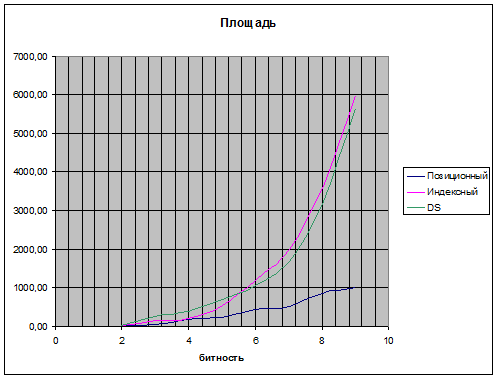
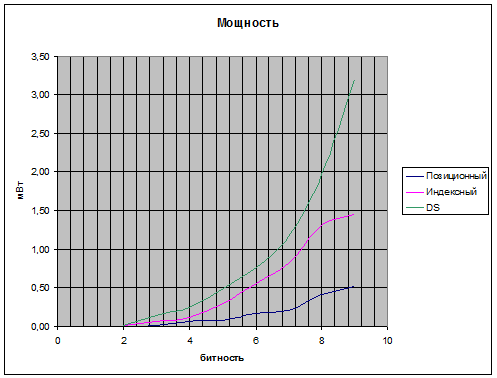
Было произведено сравнение 2 реализаций сумматоров по модулю 2n-1 - чисто комбинационная схема и схема с мультиплексированием. Сравнение производилось для модулей с разрядностью от 3 до 16 бит.

Типовые Verilog-модули

1. Сумматор с мультиплексированием (на примере 3-битного)

module sum_modulo_7 (in1, in2, out);
	input [2:0] in1;
	input [2:0] in2;
	output reg [2:0] out;
	wire [3:0] data;
	wire [3:0] data2;
	assign data = in1 + in2;
	assign data2 = in1 + in2 + 1;
	always @(*)
	begin
		if (data2[3] == 1)
			out <= data2[2:0];
		else
			out <= data[2:0];
	end
endmodule

2. Чисто комбинационный сумматор (на примере 3-битного)

module sum_modulo_7 (A, B, S);
	input [2:0] A;
	input [2:0] B;
	output[2:0] S;

	wire [2:0] G;
	wire [2:0] P;
	wire [2:0] C;

	assign G[0] = A[0]&B[0];
	assign G[1] = A[1]&B[1];
	assign G[2] = A[2]&B[2];

	assign P[0] = A[0]^B[0];
	assign P[1] = A[1]^B[1];
	assign P[2] = A[2]^B[2];

	assign C[0] = G[0] | G[2]&P[0] | G[1]&P[0]&P[2]; 
	assign C[1] = G[1] | G[0]&P[1] | G[2]&P[1]&P[0]; 
	assign C[2] = G[2] | G[1]&P[2] | G[0]&P[2]&P[1]; 

	assign S[0] = (P[0]&&(~P[2:0]))^C[2];
	assign S[1] = (P[1]&&(~P[2:0]))^C[0];
	assign S[2] = (P[2]&&(~P[2:0]))^C[1];
endmodule

Библиотека стандартных ячеек

NangateOpenCellLibrary_typical_conditional_nldm.lib

Скрипт для запуска

analyze -f verilog <имя модуля>.v
elaborate <имя модуля>
uniquify
current_design <имя модуля>
check_design
set_load [load_of [get_lib_pins NangateOpenCellLibrary/INV_X4/A]] [all_outputs]
set_driving_cell -lib_cell DFFRS_X2 -library NangateOpenCellLibrary -pin Q  [all_inputs] 
set_max_delay -to [all_outputs] 0 
set_max_area 0 
compile
report_timing -significant_digits 6 > timing_<имя модуля>.rpt
report_area > area_<имя модуля>.rpt
report_power -analysis_effort high > power_<имя модуля>.rpt
remove_design -all

Модули для эксперимента

Битность	Модуль для индексного умножителя	Модуль для DS умножителя
2	3	3
3	7	7
4	13	15
5	31	31
6	61	63
7	127	127
8	251	255
9	509	511

Результаты