Разработка модулярного КИХ фильтра на базе теоретико-числового БПФ
Цель настоящей работы состояла в том, чтобы разработать модулярный КИХ фильтр с постоянными коэффициентами, базируясь на идее "Теоремы о Свертке" и ее аналога в конечном поле Галуа.
Краткое теоретическое обоснование
Фильтр с конечной импульсной характеристикой, по своей сути, является ни чем иным, как линейной сверткой входной последовательности некоторых цифровых отсчетов с последовательностью коэффициентов фильтра. Фильтры могут быть с фиксированными и изменяемыми коэффициентами. Задача выбора тех или иных коэффициентов фильтра - сложная, и в нашей работе не рассматривается. В настоящее время существует большое количество программных продуктов, которые позволяют рассчитывать коэффициенты фильтра для различных задач.
Абстрагируясь от значений коэффициентов, обратимся непосредственно к вычислению линейной свертки. Формула для ее вычисления выглядит следующим образом:
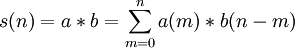 ,
, 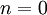 ...
... 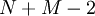
Архитектуры для вычисления линейных сверток могут быть совершенно различными. Выделяют несколько типов архитектур.
- Последовательная
- Параллельная
- Последовательно-параллельная
Последовательная схема характеризуется малым числом вычислительных блоков, интенсивным обменом с памятью и низкой производительностью. В крайнем проявлении эта схема представляет собой умножитель с накоплением и управляющее устройство, которое обеспечивает загрузку нужных коэффициентов из памяти. В этом случае, для нахождения одного выходного отсчета требуется 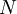 тактов. Этот метод реализуется программным методом на сигнальных процессорах или компьютерах общего назначения.
тактов. Этот метод реализуется программным методом на сигнальных процессорах или компьютерах общего назначения.
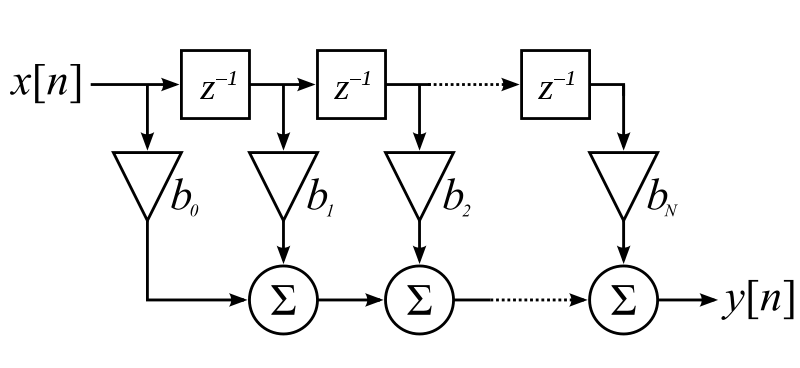
В случае, если производительности DSP процессора не хватает, то фильтр реализуют аппаратно, используя параллельные архитектуры. Параллельные схемы эксплуатируют метод конвееризации, разделяя этапы конвейера регистрами. Каноническая форма КИХ фильтра выглядит следующим образом:
Преимущества данной архитектуры - это ее быстродействие и возможность работы в реальном времени. К минусам можно отнести значительное увеличение аппаратурных затрат.
Кроме реализаций во временной области, возможна также реализация в частотной области. Базисом для этого является так называемая Теорема о Свертке. Спектр циклической свертки есть произведение спектров сворачиваемых сигналов: 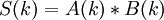 . Где
. Где 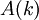 и
и 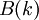 - спектры сворачиваемых сигналов,
- спектры сворачиваемых сигналов, 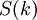 - спектр циклической свертки двух сигналов.
- спектр циклической свертки двух сигналов.
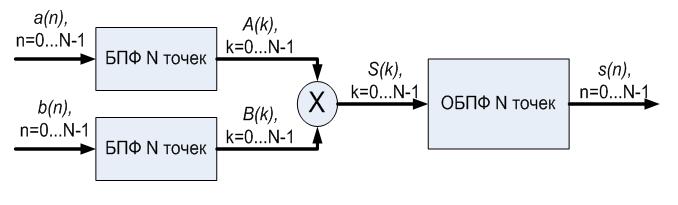
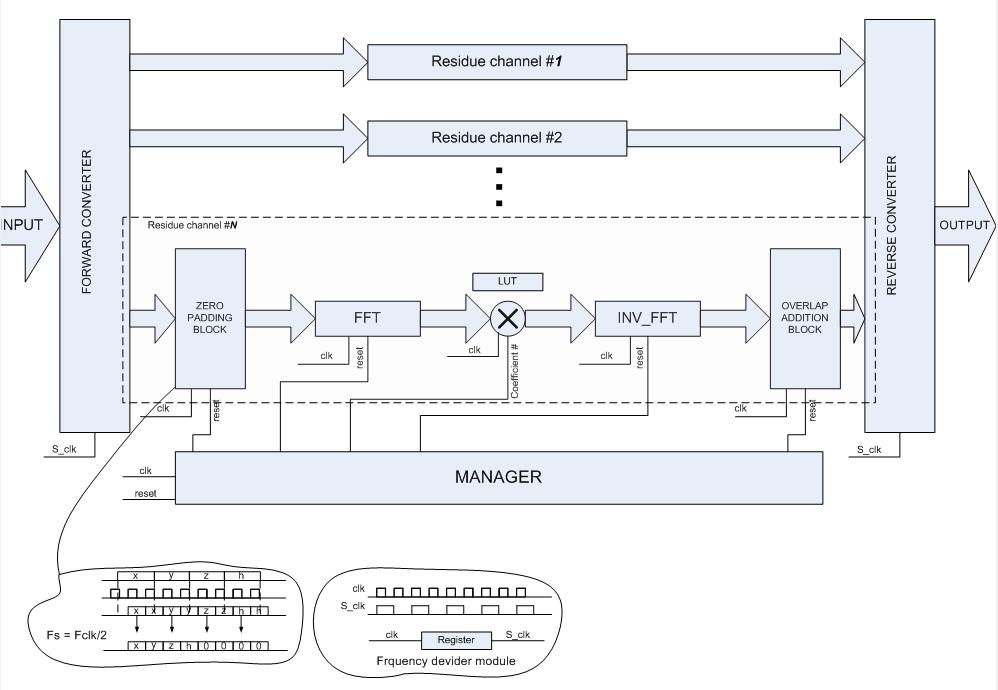
Таким образом, вместо того чтобы реализовывать свертку непосредственно по формуле, можно перевести сигналы в частотную область с помощью БПФ, там почленно перемножить, и перевести обратно. Результат будет соответствовать циклической свертке [статья в ростове]. Дополняя нулями последовательности, вычисление циклической свертки станет эквивалентно вычислению искомой линейной свертки. Преимуществом этого метода является сокращение операций. Действительно, используя быстрые схемы преобразования Фурье, мы тратим лишь 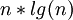 операций, что дает выигрых при больших значениях
операций, что дает выигрых при больших значениях 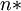 .
.