Разработка модулярного КИХ фильтра на базе теоретико-числового БПФ
Цель настоящей работы состояла в том, чтобы разработать модулярный КИХ фильтр с постоянными коэффициентами, базируясь на идее "Теоремы о Свертке" и ее аналога в конечном поле Галуа.
Краткое теоретическое обоснование
Фильтр с конечной импульсной характеристикой, по своей сути, является ни чем иным, как линейной сверткой входной последовательности некоторых цифровых отсчетов с последовательностью коэффициентов фильтра. Фильтры могут быть с фиксированными и изменяемыми коэффициентами. Задача выбора тех или иных коэффициентов фильтра - сложная, и в нашей работе не рассматривается. В настоящее время существует большое количество программных продуктов, которые позволяют рассчитывать коэффициенты фильтра для различных задач.
Абстрагируясь от значений коэффициентов, обратимся непосредственно к вычислению линейной свертки. Формула для ее вычисления выглядит следующим образом:
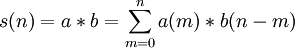 ,
, 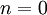 ...
... 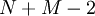
Архитектуры для вычисления линейных сверток могут быть совершенно различными. Выделяют несколько типов архитектур.
- Последовательная
- Параллельная
- Последовательно-параллельная
Последовательная схема характеризуется малым числом вычислительных блоков, интенсивным обменом с памятью и низкой производительностью. В крайнем проявлении эта схема представляет собой умножитель с накоплением и управляющее устройство, которое обеспечивает загрузку нужных коэффициентов из памяти. В этом случае, для нахождения одного выходного отсчета требуется 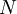 тактов. Этот метод реализуется программным методом на сигнальных процессорах или компьютерах общего назначения.
тактов. Этот метод реализуется программным методом на сигнальных процессорах или компьютерах общего назначения.
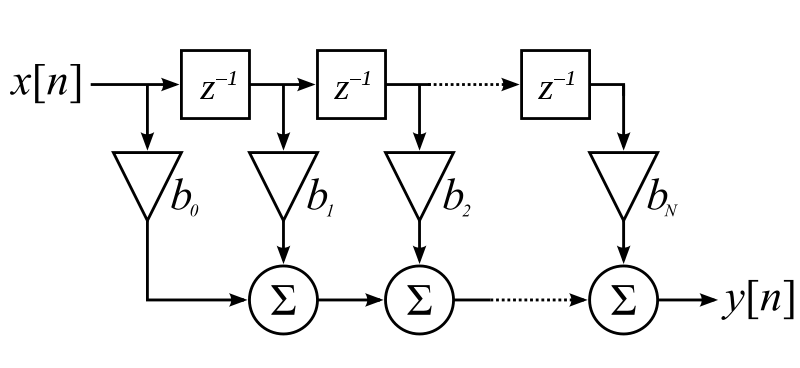
В случае, если производительности DSP процессора не хватает, то фильтр реализуют аппаратно, используя параллельные архитектуры. Параллельные схемы эксплуатируют метод конвееризации, разделяя этапы конвейера регистрами. Каноническая форма КИХ фильтра выглядит следующим образом:
Преимущества данной архитектуры - это ее быстродействие и возможность работы в реальном времени. К минусам можно отнести значительное увеличение аппаратурных затрат.
Кроме реализаций во временной области, возможна также реализация в частотной области. Базисом для этого является так называемая Теорема о Свертке. Спектр циклической свертки есть произведение спектров сворачиваемых сигналов: 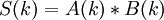 . Где
. Где 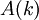 и
и 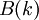 - спектры сворачиваемых сигналов,
- спектры сворачиваемых сигналов, 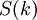 - спектр циклической свертки двух сигналов.
- спектр циклической свертки двух сигналов.
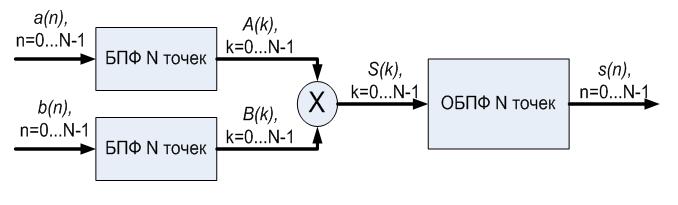
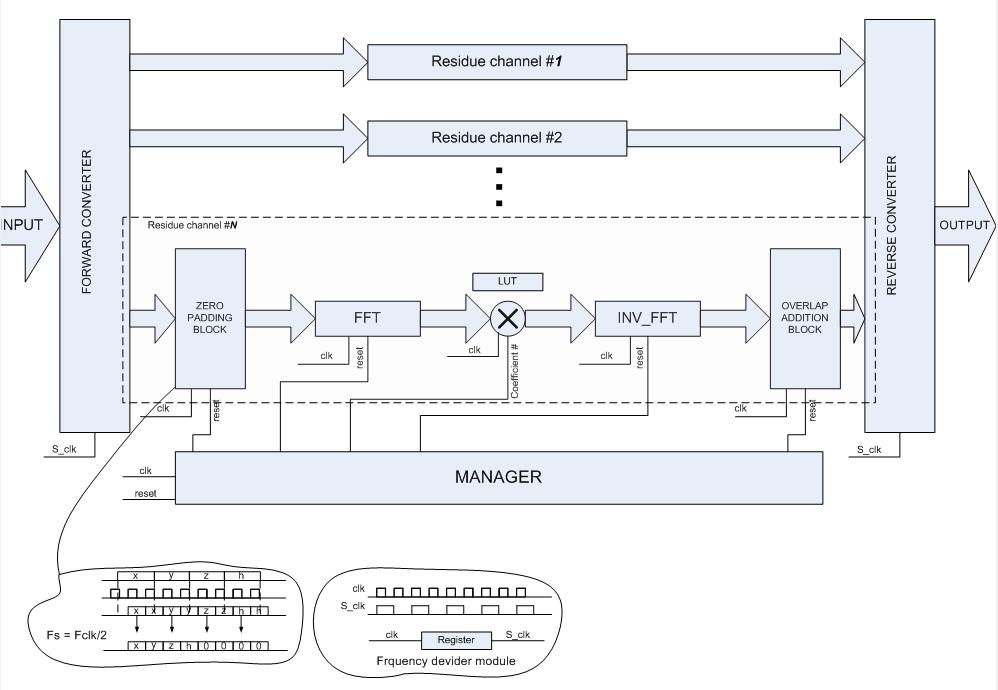
Таким образом, вместо того чтобы реализовывать свертку непосредственно по формуле, можно перевести сигналы в частотную область с помощью БПФ, там почленно перемножить, и перевести обратно. Результат будет соответствовать циклической свертке [статья в ростове]. Дополняя нулями последовательности, вычисление циклической свертки станет эквивалентно вычислению искомой линейной свертки. Преимуществом этого метода является сокращение операций. Действительно, используя быстрые схемы преобразования Фурье, мы тратим лишь 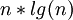 операций, что дает выигрых при больших значениях
операций, что дает выигрых при больших значениях  .
.
Однако, существуют и недостатки. Зачастую в фильтрах подразумевается входной сигнал бесконечной длительности, который фильтруется некоторым ограниченным набором коэффициентов. Параллельная схема отлично справляется с этой задачей в "онлайн" режиме. С методами на основе БПФ дело обстоит сложнее. Во первых не возможно создать БПФ на бесконечное число точек, а во вторых, даже если мы создадим очень большой преобразователь, то мы потеряем "онлайн" режим, так как для того чтобы БПФ начал выдавать значения, нам необходимо чтобы все значения были туда загружены. Чтобы решить данную проблему были введены различные "overlap" методики. Они позволяют обрабатывая блоки малого размера, совмещать их таким образом, чтобы на выходе мы получили необходимую свертку теоретически бесконечной последовательности отсчетов [та презенташка с оверлап методиками].
Резюмируя вышесказанное, что касается методов фильтрации в частотной области, можно отметить что в принципе этот метод можно также реализовывать как в последовательном так и в параллельном виде. Для параллельного метода можно использовать различные конвейерные методики реализации БПФ (типа Radix-2 SPDF). Последовательные методы реализуются программно. Судя по всему, чаще всего эта методика используется именно в последовательной реализации в виде программ на микроконтроллерах и компьютерах общего назначения. Условно классифицировать методы реализации КИХ фильтров можно следующим образом:
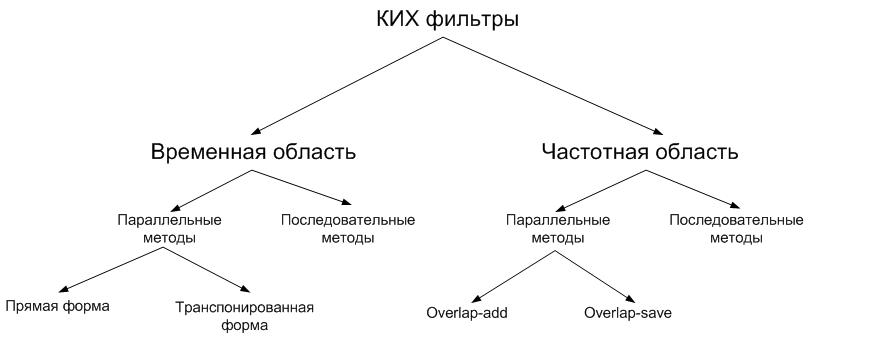
Для реализации фильтров, а в общем и других устройств ЦОС, эффективно использовать аппарат модулярной арифметики. Можно использовать модулярную арифметику при реализации любого КИХ фильтра, реализованного любым методом. Однако, наибольший интерес представляет использование модулярной арифметики при параллельной реализации в частотной области. Существует несколько предпосылок для этого вывода, основная из которых заключается в том, что для конечных полей существует аналог теоремы о свертке. Точнее говоря, для конечных полей существует преобразование, аналогичное преобразованию Фурье для которого выполняется теорема о свертке в конечном поле, и для которого соблюдаются все симметрические свойства позволяющие использовать любой быстрый алгоритм для его вычисления. Формула упомянутого преобразования выглядит следующим образом:
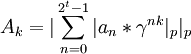
Здесь 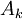 - теоретико-числовой спектр сигнала,
- теоретико-числовой спектр сигнала, 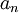 - сам сигнал,
- сам сигнал,  - характеристика конечного поля,
- характеристика конечного поля, 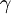 - примитивный корень степени
- примитивный корень степени 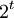 [Виноградов, Теория чисел]. Если число
[Виноградов, Теория чисел]. Если число  имеет вид
имеет вид 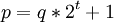 , то примитивный корень степени
, то примитивный корень степени 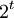 - всегда существует и равен
- всегда существует и равен 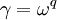 .
.
Таким образом, упомянутое преобразованиек является аналогом дискретного преобразования Фурье тригонометрического базиса, в котором поворачивающие множители 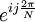 заменяются на
заменяются на 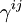 , а операции умножения и сложения комплексных чисел – на соответствующие операции в
, а операции умножения и сложения комплексных чисел – на соответствующие операции в 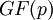 .
.
Кроме очевидных преимуществ в виде распараллеливания вычислений, мы достигаем большей точности, так как вычисления ведутся в конечных молях с целыми поворачивающими множителями, что исключает ошибки представления, характерные для стандартного тригонометрического метода.