Пример коррекции ошибки на базе системы остаточных классов
Постановка задачи
В данной статье разбирается пример работы алгоритма коррекции ошибки для 16-битных строк. Числовое значение строки представляется в модулярном базисе состоящем из 4-5-битных простых чисел (аналог 4-х битного блока в позиционных кодах). Необходимо отследить и исправить одиночную ошибку, внесённую в один из модулярных каналов.
Любой строке из 16 бит можно поставить в соответствие число из диапазона 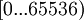 . Далее данное число мы представляем в системе остаточных классов (СОК) по выбранным нами модулям. Затем, внеся одиночную ошибку в любой модуль мы попробуем исправить её. Алгоритм исправления ошибки заключается в следующем: последовательно исключаем из рассмотрения один из модулей, восстанавливаем число по Китайской Теореме об Остатках и смотрим на величину полученного числа.
. Далее данное число мы представляем в системе остаточных классов (СОК) по выбранным нами модулям. Затем, внеся одиночную ошибку в любой модуль мы попробуем исправить её. Алгоритм исправления ошибки заключается в следующем: последовательно исключаем из рассмотрения один из модулей, восстанавливаем число по Китайской Теореме об Остатках и смотрим на величину полученного числа.
Теоретические основы алгоритма
Пусть имеется 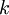 взаимно простых чисел
взаимно простых чисел 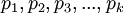 . Назовём их рабочими основаниями. Известно, что в СОК по данным модулям однозначно представляется число из рабочего диапазона
. Назовём их рабочими основаниями. Известно, что в СОК по данным модулям однозначно представляется число из рабочего диапазона 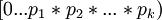 . Далее введём два дополнительных взаимно простых основания
. Далее введём два дополнительных взаимно простых основания 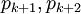 таких, что все
таких, что все 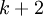 полученных оснований
полученных оснований 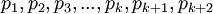 будут взаимно простыми. Пусть наше исходное число
будут взаимно простыми. Пусть наше исходное число  принадлежит диапазону
принадлежит диапазону 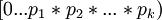 . Если представить его в СОК по модулям
. Если представить его в СОК по модулям 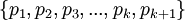 , затем внести ошибку по любому из модулей, а потом попытаться восстановить данное число по Китайской Теореме об Остатках, то известно, что результат
, затем внести ошибку по любому из модулей, а потом попытаться восстановить данное число по Китайской Теореме об Остатках, то известно, что результат 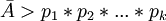 . Таким образом, имея два контрольных основания мы можем исправлять одиночную ошибку, последовательно исключая по одному из модулей и получая ситуацию, описанную выше. Если мы исключили основание, по которому произошла ошибка, мы получим правильное число, лежащее в пределах диапазона
. Таким образом, имея два контрольных основания мы можем исправлять одиночную ошибку, последовательно исключая по одному из модулей и получая ситуацию, описанную выше. Если мы исключили основание, по которому произошла ошибка, мы получим правильное число, лежащее в пределах диапазона 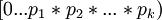 .
.
Пример
Пусть имеется 16ти-битная строка 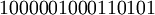 . Мы ставим ей в соответствие число, затем представляем его в Системе Остаточных Классов, вносим ошибку по одному из оснований и исправляем эту ошибку.
. Мы ставим ей в соответствие число, затем представляем его в Системе Остаточных Классов, вносим ошибку по одному из оснований и исправляем эту ошибку.
Шаг 1
Для выполнения данной задачи выбираем 4 рабочих основания и 2 контрольных.
Рабочие основания: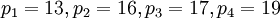 . Контрольные основания:
. Контрольные основания: 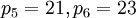 .
При таком выборе рабочих оснований мы можем работать с числами из диапазона от
.
При таком выборе рабочих оснований мы можем работать с числами из диапазона от 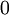 до
до 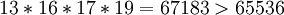 . Таким образом, этих рабочих оснований хватит для работы с нашей исходной строкой.
Выбор таких рабочих обусловлен тем, что полученный динамический диапазон практически совпадает с исходным
. Таким образом, этих рабочих оснований хватит для работы с нашей исходной строкой.
Выбор таких рабочих обусловлен тем, что полученный динамический диапазон практически совпадает с исходным 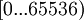 . Изначально строка содержала 16 бит, но после кодирования (представления строки в СОК и перевода обратно в двоичную системы) мы получим строку длиной
. Изначально строка содержала 16 бит, но после кодирования (представления строки в СОК и перевода обратно в двоичную системы) мы получим строку длиной 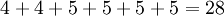 .
Таким образом, избыточность составляет
.
Таким образом, избыточность составляет 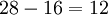 бит. Представим это число в СОК:
бит. Представим это число в СОК:
Шаг 2
Процесс кодирования и внесения ошибки:
Переведем строку 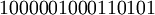 в десятичную систему счисления и получим
в десятичную систему счисления и получим 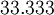
Представим это число в СОК по нашим модулям и получим: 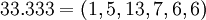 . Представим всё это в бинарном виде:
. Представим всё это в бинарном виде:
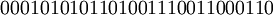 . Это и есть наша закодированная строка. Затем внесем ошибку по одному из оснований. Для данного примера я выбрал пятое основание, т.е. 21. В результате ошибки мы получим строку, с которой и будет работать декодер.
. Это и есть наша закодированная строка. Затем внесем ошибку по одному из оснований. Для данного примера я выбрал пятое основание, т.е. 21. В результате ошибки мы получим строку, с которой и будет работать декодер.
Шаг 3
Теперь рассмотрим процесс декодирования:
На данном этапе мы хотим выяснить: произошла ли ошибка по какому-либо основанию и если произошла, то исправить эту ошибку.
Рассмотрим строку, полученную в результате кодирования и внесения ошибки:
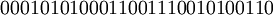 .
.
Представим число, соответствующее данной строке, в СОК по нашим модулям:
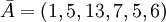 .
Теперь отбрасываем последовательно по одному основанию и смотрим результат. Если он меньше 67183, то мы принимаем этот результат за исходное число, а по отброшенному основанию произошла ошибка. Пусть мы откидываем первое основание. Тогда по пяти оставшимся мы восстанавливаем число. Получаем систему сравнений:
.
Теперь отбрасываем последовательно по одному основанию и смотрим результат. Если он меньше 67183, то мы принимаем этот результат за исходное число, а по отброшенному основанию произошла ошибка. Пусть мы откидываем первое основание. Тогда по пяти оставшимся мы восстанавливаем число. Получаем систему сравнений:
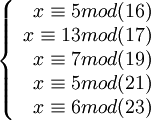
Согласно Китайской Теореме об Остатках данная система имеет одно единственное решение в диапазоне от 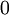 до
до 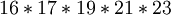
Решением данной системы является число 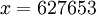 . Видим, что число находится вне нашего диапазона, а следовательно по одному из неотброшенных оснований произошла ошибка, а по отброшенному основанию ошибки нет.
. Видим, что число находится вне нашего диапазона, а следовательно по одному из неотброшенных оснований произошла ошибка, а по отброшенному основанию ошибки нет.
Теперь отбросим основание 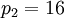 . Проделывая те же действия, что и для первого основания получим, что
. Проделывая те же действия, что и для первого основания получим, что 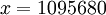 . Опять мы вышли за допустимый диапазон, а следовательно по второму основанию ошибки нет.
. Опять мы вышли за допустимый диапазон, а следовательно по второму основанию ошибки нет.
Отбрасывая третье основание 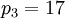 , получим
, получим 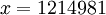 .
.
Отбрасывая четвертое основание 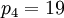 , получим
, получим 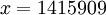
Отбрасывая пятое основание 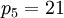 , получим
, получим 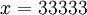 . Полученное число попадает в динамический диапазон, а следовательно, является нашим верным числом.
Таким образом мы нашли и разряд, в котором произошла ошибка, а именно блок, отвечающий за остаток по модулю 21, ведь именно этот блок мы исключили на данном этапе восстановления.
. Полученное число попадает в динамический диапазон, а следовательно, является нашим верным числом.
Таким образом мы нашли и разряд, в котором произошла ошибка, а именно блок, отвечающий за остаток по модулю 21, ведь именно этот блок мы исключили на данном этапе восстановления.
