Бимодульная модулярная арифметика
Аддитивный характер вычислений в кольце вычетов 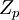 порождает дополнительные расходы на выполнение арифметических операций. Это обусловлено тем, что результат выполненной операции может выйти за диапазон
порождает дополнительные расходы на выполнение арифметических операций. Это обусловлено тем, что результат выполненной операции может выйти за диапазон 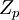 , тогда требуется корректировка результата, т.е. взятие результата выполненной операции по модулю. Мультипликативная операция над остатками x, y mod p более трудоемка, поэтому наиболее эффективным способом избежать прямой реализации мультипликативной операции является переход к индексам вычетов по основанию первообразного корня, однозначно связанных с данным модулярным кодом.
, тогда требуется корректировка результата, т.е. взятие результата выполненной операции по модулю. Мультипликативная операция над остатками x, y mod p более трудоемка, поэтому наиболее эффективным способом избежать прямой реализации мультипликативной операции является переход к индексам вычетов по основанию первообразного корня, однозначно связанных с данным модулярным кодом.
В случае индексной арифметики операция «+» выполняется за один такт модульного суммирования, а операция «*» за такт модульного суммирования и два такта табличной операции. Для того, чтобы сбалансировать выполнение модульных операций Д.А. Поспелов ввел представление исходных операндов в виде пар 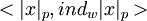 >, где
>, где 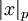 есть вычет
есть вычет  по модулю
по модулю  ,
, 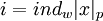 - соответствующий вычету
- соответствующий вычету 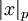 индекс, при этом условно считается, что вычету 0 соответствует специальный символ λ, который обладает свойством λ+i=i+λ для любого для любого индекса
индекс, при этом условно считается, что вычету 0 соответствует специальный символ λ, который обладает свойством λ+i=i+λ для любого для любого индекса 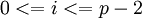 . Таким образом, все операции поля выполняются над парами: если требуется найти сумму двух операндов по модулю
. Таким образом, все операции поля выполняются над парами: если требуется найти сумму двух операндов по модулю  , то суммируются по модулю
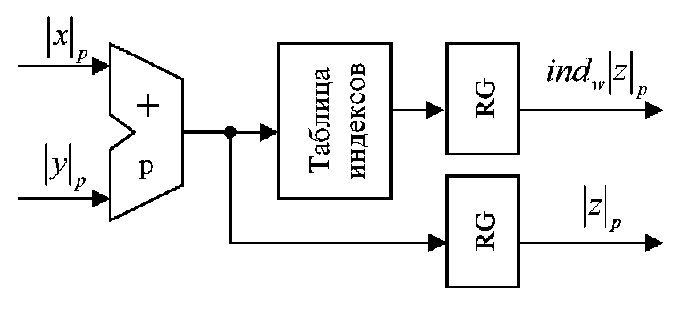
, то суммируются по модулю  первые компоненты пар; для формирования второй компоненты пары результата этот результат преобразуется в индекс путем выборки значения из таблицы индексов (рис.1). Если требуется найти произведение двух операндов по модулю
первые компоненты пар; для формирования второй компоненты пары результата этот результат преобразуется в индекс путем выборки значения из таблицы индексов (рис.1). Если требуется найти произведение двух операндов по модулю  , то суммируются по модулю
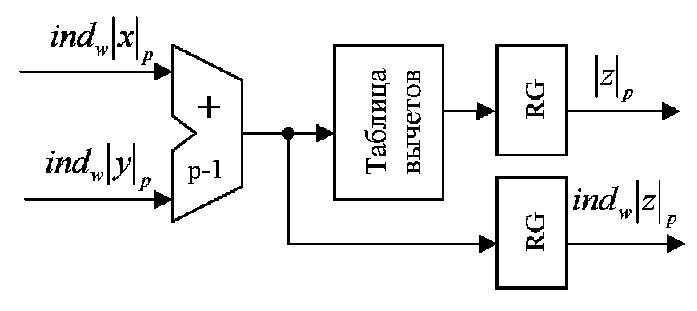
, то суммируются по модулю 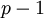 вторые компоненты пар; для формирования первой компоненты пары результата этот результат преобразуется в антилогарифм (вычет) путем выборки значения из таблицы вычетов (рис.2):
вторые компоненты пар; для формирования первой компоненты пары результата этот результат преобразуется в антилогарифм (вычет) путем выборки значения из таблицы вычетов (рис.2):