Метод инжектирования ошибок для оценки надежностных характеристик комбинационных схем
Содержание
Введение
Суть метода заключается в том, что в процессе моделирования исследуемой логической схемы в один или несколько узлов схемы вносится ошибка. Необходимо определить: произошло ли искажение результата работы схемы, и была ли ошибка обнаружена.
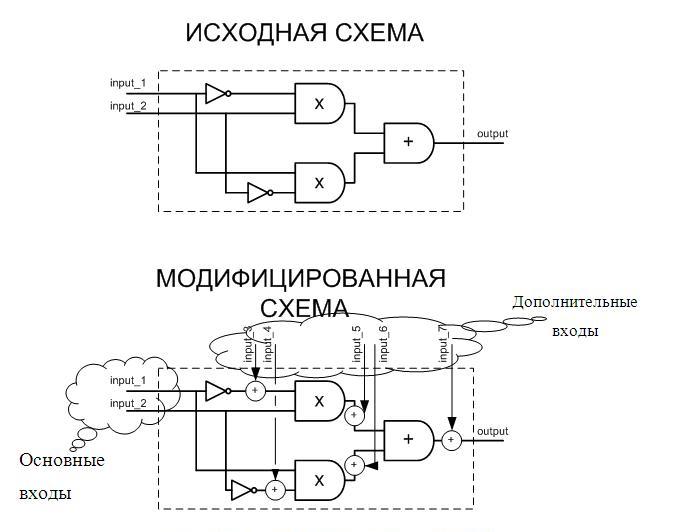
Предлагаемый подход инжектирования ошибок при логическом моделировании подразумевает модификацию схемы таким образом, чтобы появилась возможность вносить ошибки в любой узел схемы. Для этого после каждого вентиля в схему необходимо добавить дополнительный элемент, называемый инжектором. Процесс модификации схемы на примере логической функции XOR в базисе И-ИЛИ-НЕ представлен на рисунке:
Первый вход инжектора соединяется с выходом вентиля, выход инжектора подается в соответствии с начальной коммутацией схемы. Второй входной сигнал инжектора определяется как входной сигнал основной схемы и интерпретируется как дополнительный вход. Логическая единица на любом дополнительном входе – означает ошибку в соответствующем ей вентиле. Инжектор выполняет бинарную логическую операцию, формируемую в зависимости от типа моделируемой ошибки.
Типы моделируемых ошибок
Чаще всего в литературе, связанной с помехоустойчивостью логических схем, рассматриваются только ошибки, связанные с инверсией сигнала. Однако, часто на практике приходится встречаться с ошибками, обусловленными технологическими несовершенствами микроэлектронных изделий, таких как замыкания. В этой работе мы будем рассматривать три основных типа ошибок:
• Замыкание на питание (stuck at VCC);
• Замыкание на землю (stuck on ground);
• Инверсия сигнала.
Структура модифицированной схемы, в зависимости от типа ошибок, существенно изменяться не будет, поменяются только двухвходовые логические элементы эмулирующие ошибку в вентиле. Типы элементов с таблицами истинности для каждого типа ошибки представлены в таблице:
Тип ошибки |
Таблица истинности для инжектора |
Название булевой функции инжектора |
|||||||||||||||
Замыкание на питание (stuck at VCC); |
|
OR, Логическое ИЛИ |
|||||||||||||||
Замыкание на землю (stuck on ground); |
|
Инверсия прямой импликации (больше, детектор 4 |
|||||||||||||||
Инверсия сигнала |
|
XOR, Сумма по модулю 2, Исключающее ИЛИ |
Метод статистического внесения сбоев заключается в использовании метода Монте-Карло [8], что подразумевает проведение многократных экспериментов с различными входными данными с последующей оценкой необходимых параметров отказоустойчивости.
Модели возникновения ошибок
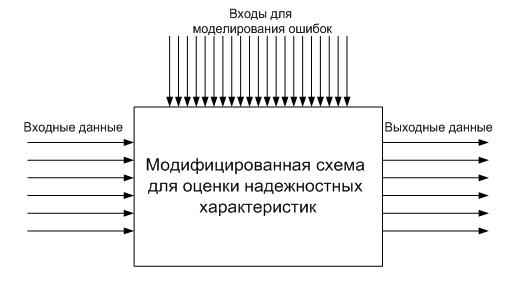
В общем виде, схему для оценки помехоустойчивости можно представить в следующем виде:
Пусть входы для моделирования ошибок формируют вектор ошибки:
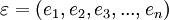 , где
, где 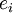 –
– 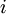 -ый вход. При
-ый вход. При 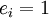 в схему внедряется ошибка в
в схему внедряется ошибка в 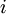 -ый вентиль. При
-ый вентиль. При 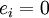 - ошибки нет.
- ошибки нет.
Шум окружающей среды
При реализации этой стратегии внесения ошибок будем рассматривать ситуацию, когда каждый вентиль имеет некоторую вероятность сбоя. Для удобства эта вероятность фиксируется для всех вентилей схемы, а ошибки происходят независимо.
Таким образом, введем некоторый вещественный параметр ![\gamma \in [0,1]](/w/images/math/e/e/1/ee133ef1a28ae6f8bcf231e9dca9c222.png) , который будет являться характеристикой шума окружающей среды. Тогда элемент
, который будет являться характеристикой шума окружающей среды. Тогда элемент 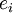 при каждой подаче входных воздействий с вероятностью
при каждой подаче входных воздействий с вероятностью 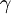 может обратиться в единицу. При таком подходе количество ошибок в схеме, при одной подаче данных, лежит в диапазоне от нуля до общего числа элементов схемы
может обратиться в единицу. При таком подходе количество ошибок в схеме, при одной подаче данных, лежит в диапазоне от нуля до общего числа элементов схемы  . Случаи с нулевым вектором ошибки при подсчетах характеристик помехоустойчивости схемы не рассматриваются.
. Случаи с нулевым вектором ошибки при подсчетах характеристик помехоустойчивости схемы не рассматриваются.
Кратные ошибки
Фиксируется параметр 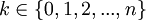 – кратность ошибки. Вектор
– кратность ошибки. Вектор 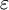 при каждой подаче входных воздействий генерируется случайным образом так, чтобы вес его всегда был равен
при каждой подаче входных воздействий генерируется случайным образом так, чтобы вес его всегда был равен 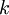 . Пример векторов для
. Пример векторов для 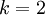 :
:
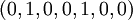
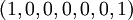
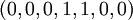

Стресс-тесты для определенных вентилей
Кроме нахождения обобщенных характеристик отказоустойчивости схемы, метод инжектирования ошибок может быть полезен для выявления наиболее уязвимых участков схемы с точки зрения влияния ошибки в конкретном вентиле на общую работоспособность. Эмпирически было установлено существенное различие в уязвимости для разных участков типовых схем. Этот факт привод к идее разработки методов селективной избыточности комбинационных схем. Эффективным методом определения степени уязвимости участка схемы может служить метод инжектирования ошибок с использованием стратегии стресс-теста:
- Фиксируется элемент 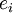 , который на всем протяжении тестирования будет равен единице. Остальные элементы вектора
, который на всем протяжении тестирования будет равен единице. Остальные элементы вектора 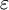 обращены в ноль.
- Определяется влияние конкретного вентиля (группы вентилей) на корректность работы всей схемы в условиях помех.
Селективное добавление избыточности для наиболее уязвимых участков схемы позволит достичь разумного компромисса в надежности функционирования при незначительном увеличении площади микросхемы.
обращены в ноль.
- Определяется влияние конкретного вентиля (группы вентилей) на корректность работы всей схемы в условиях помех.
Селективное добавление избыточности для наиболее уязвимых участков схемы позволит достичь разумного компромисса в надежности функционирования при незначительном увеличении площади микросхемы.
Характеристики помехозащищенности схемы
Для оценки архитектурной устойчивости к сбоям и отказам, а также для оценки эффективности методов исправления ошибок в процессе моделирования необходимо подсчитывать следующие параметры:
- общее количество экспериментов;
- количество корректных значений выхода схемы;
- общее количество внедренных ошибок.
После проведения серии экспериментов в количестве, достаточном для получения корректной статистической выборки, необходимо вычислить характеристики, с помощью которых можно эффективно сравнивать между собой различные архитектуры комбинационных схем с точки зрения их помехозащищенности.
Для оценки отказоустойчивости схем с точки зрения исправления ошибок будем рассматривать два параметра. Первый параметр характеризует архитектурную устойчивость к ошибкам и определяется как отношение числа некорректных результатов работы схемы к общему числу инжектированных ошибок:
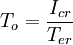
где 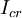 - количество экспериментов с несовпадением результата с эталонным,
- количество экспериментов с несовпадением результата с эталонным, 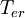 - общее число внедренных ошибок. По сути, этот параметр определяет вероятность того, что внедренная ошибка в схему приведет к искажению работы всей схемы.
Второй параметр определяет общую устойчивость схемы к ошибкам и вычисляется как отношение числа корректных результатов работы схемы к общему числу тестов:
- общее число внедренных ошибок. По сути, этот параметр определяет вероятность того, что внедренная ошибка в схему приведет к искажению работы всей схемы.
Второй параметр определяет общую устойчивость схемы к ошибкам и вычисляется как отношение числа корректных результатов работы схемы к общему числу тестов:
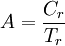
В случае комбинационных схем, обнаруживающих ошибки, мы располагаем не только эталонным значением выхода схемы, но и эталонным значением флага ошибки на заданных входных данных. Таким образом, в процессе моделирования необходимо подсчитывать число появлений для событий, описанных в таблице:
Истинность результата (0 – результат верный 1 – результат не верный) |
Флаг ошибки |
Событие |
0 |
0 |
Ошибка не «проявилась» |
0 |
1 |
«Ложная тревога» |
1 |
0 |
Ошибка пропущена |
1 |
1 |
Ошибка обнаружена |
Следует отметить, что при каждой подаче данных в процессе моделирования, в схему вносится, по меньшей мере, одна ошибка. В этом контексте первую строку таблицы 3 следует понимать, как некоторую способность архитектуры маскировать ошибки, то есть ошибка, возникшая на одном из вентилей схемы, не доходит до выходов из-за особенностей её архитектуры. Эти четыре варианта составляют полную группу событий, следовательно, характеристиками помехоустойчивости схемы будут являться вероятности наступления каждого из событий.