Китайская теорема об остатках
Китайская теорема об остатках формулируется следующим образом:
Теорема.
Пусть 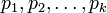 - попарно взаимно простые числа, большие 1, и пусть
- попарно взаимно простые числа, большие 1, и пусть 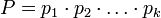 . Тогда существует единственное неотрицательное решение по модулю
. Тогда существует единственное неотрицательное решение по модулю 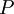 следующей системы сравнений:
следующей системы сравнений:
-
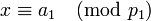 ,
,
-
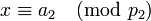 ,
,
-
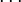 ,
,
-
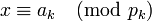 .
.
Другими словами, отображение, которое каждому целому числу  ,
, 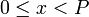 , ставит в соответствие кортеж
, ставит в соответствие кортеж 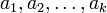 , где
, где 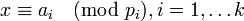 является биекцией кольца
является биекцией кольца 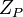 на декартово произведение
на декартово произведение 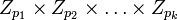 колец
колец 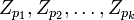 .
.
Т.е. соответствие между числами и кортежами является взаимно однозначным, кроме того, операции, выполняемые над числом  , можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом:
, можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом:
если
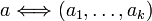 ,
,
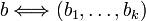 ,
,
то справедливо:
-
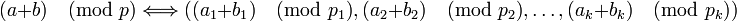 ,
,
-
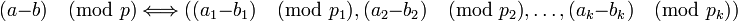 ,
,
-
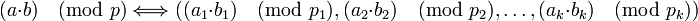 .
.
Существует много различных доказательств китайской теоремы об остатках. Приведём конструктивное доказательство этой теоремы.