Представление числа в системе остаточных классов
Представление чисел в виде набора остатков от деления на выбранные натуральные модули - основания системы называется системой остаточных классов - СОК (residue number system - RNS) или модулярной системой счисления - МСС (modular system).
Такие системы счисления являются непозиционными кодами с параллельной структурой, которые позволяют реализовать идею распараллеливания операций на уровне выполнения элементарных арифметических действий.
Пусть заданы положительные числа
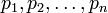 , которые называют основаниями или модулями системы. Обозначим
, которые называют основаниями или модулями системы. Обозначим
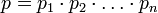 .
.
Эта величина характеризует объём диапазона системы. Под системой остаточных классов понимают такую непозиционную систему счисления, в которой целое неотрицательное число А можно представить в виде набора остатков от деления этого числа на выбранные основания системы, т. е.
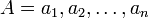 , где
, где ![a_i = A-[ \frac {A}{p_i}]\cdot p_i, i=1,\ldots ,n](/w/images/math/c/e/1/ce1e09b0b177115b289b00d0df953b5b.png) .
.
Возможность такого представления числа определяется теоремой о делении с остатком в кольце целых чисел. Напомним формулировку этой теоремы (в обозначениях этого раздела).
Теорема
Если
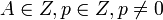 ,
то существуют единственные
,
то существуют единственные
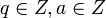 ,
такие, что
,
такие, что
![A=qp+a, 0 \le a < |p|, q=[\frac {A}{p}]](/w/images/math/2/7/3/273e3c10b3ce4a23eb35a35291527f4b.png) .
.
Несложно заметить, что каждый остаток 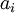 получается независимо от других и содержит информацию обо всём числе.
Установить взаимно-однозначное соответствие между целыми числами из диапазона
получается независимо от других и содержит информацию обо всём числе.
Установить взаимно-однозначное соответствие между целыми числами из диапазона 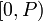 и их остатками позволяет китайская теорема об остатках.
Возможность применения СОК в вычислительных алгоритмах обуславливается наличием определённого изоморфизма между математическими операциями над целыми числами и соответствующими операциями над системой целых неотрицательных остатков по отдельным модулям. Причём сложение, умножение, возведение в целую положительную степень любых целых положительных чисел совершенно идентичны соответствующим операциям, выполняемым над системой остатков.
и их остатками позволяет китайская теорема об остатках.
Возможность применения СОК в вычислительных алгоритмах обуславливается наличием определённого изоморфизма между математическими операциями над целыми числами и соответствующими операциями над системой целых неотрицательных остатков по отдельным модулям. Причём сложение, умножение, возведение в целую положительную степень любых целых положительных чисел совершенно идентичны соответствующим операциям, выполняемым над системой остатков.
Пусть операнды  и
и 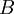 , а также результаты операций сложения и умножения
, а также результаты операций сложения и умножения 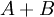 и A\cdot B</math> представлены соответственно остатками
и A\cdot B</math> представлены соответственно остатками
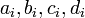 по основаниям
по основаниям 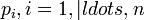 ,
причём оба числа и результаты находятся в диапазоне
,
причём оба числа и результаты находятся в диапазоне 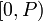 , то есть
, то есть
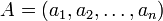 ,
,
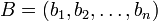 ,
,
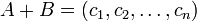 ,
,
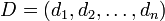 ,
,
и
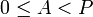 ,
, 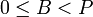 ,
,  ,
, 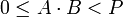 .
.
Эти выражения можно переписать в виде
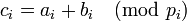 ;
;
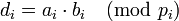 ;
;
![c_i=a_i+b_i - [\frac{a_i+b_i}{p_i}]](/w/images/math/b/b/9/bb9663abced3dcb5d8747b511a0ca7a0.png) ;
;
![d_i=a_i\cdot b_i - [\frac{a_i\cdot b_i}{p_i}]](/w/images/math/e/d/c/edcaa88c5becb67414f1a037379a726c.png) ;
;
Справедливость этих правил выполнения арифметических действий в СОК непосредственно вытекает из свойств сравнения.