Модульные операции
Материал из Модулярная арифметики
Возможность применения СОК в вычислительных алгоритмах обусловлено наличием определённого изоморфизма между математическими операциями над целыми числами и соответствующими операциями над системой целых неотрицательных остатков по отдельным модулям. Сложение, умножение, возведение в целую положительную степень любых целых положительных чисел идентичны соответствующим операциям, выполняемым над системой остатков.
Пусть операнды  и
и 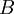 , а также результаты операций сложения и умножения
, а также результаты операций сложения и умножения 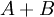 и
и 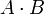 представлены соответственно остатками
представлены соответственно остатками 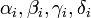 по основаниям
по основаниям 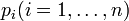 , причём оба числа и результаты находятся в диапазоне
, причём оба числа и результаты находятся в диапазоне 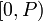 , то есть
, то есть
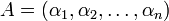 ,
,
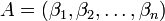 ,
,
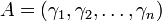 ,
,
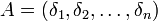
и
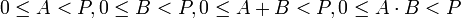 .
.
<to be continued>