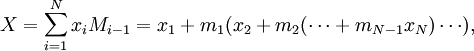–Я–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Є–є –Ї–Њ–і
(–Э–Њ–≤–∞—П —Б—В—А–∞–љ–Є—Ж–∞: ¬Ђ'''–Я–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Є–є –Ї–Њ–і''' (–Є–ї–Є —Б–Є—Б—В–µ–Љ–∞ —Б—З–Є—Б–ї–µ–љ–Є—П —Б–Њ —Б–Љ–µ—И–∞–љ–љ—Л–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ –Њ—В –∞–љ–≥–ї. [http://en.wikipediaвА¶¬ї) |
|||
| –°—В—А–Њ–Ї–∞ 10: | –°—В—А–Њ–Ї–∞ 10: | ||
* –°—А–∞–≤–љ–µ–љ–Є—П —З–Є—Б–µ–ї | * –°—А–∞–≤–љ–µ–љ–Є—П —З–Є—Б–µ–ї | ||
* –Я–µ—А–µ–≤–Њ–і–∞ —З–Є—Б–µ–ї –Є–Ј —Б–Є—Б—В–µ–Љ—Л –Њ—Б—В–∞—В–Њ—З–љ—Л—Е –Ї–ї–∞—Б—Б–Њ–≤ –≤ –Њ–±—Л—З–љ—Г—О –њ–Њ–Ј–Є—Ж–Є–Њ–љ–љ—Г—О —Б–Є—Б—В–µ–Љ—Г —Б—З–Є—Б–ї–µ–љ–Є—П | * –Я–µ—А–µ–≤–Њ–і–∞ —З–Є—Б–µ–ї –Є–Ј —Б–Є—Б—В–µ–Љ—Л –Њ—Б—В–∞—В–Њ—З–љ—Л—Е –Ї–ї–∞—Б—Б–Њ–≤ –≤ –Њ–±—Л—З–љ—Г—О –њ–Њ–Ј–Є—Ж–Є–Њ–љ–љ—Г—О —Б–Є—Б—В–µ–Љ—Г —Б—З–Є—Б–ї–µ–љ–Є—П | ||
| + | |||
| + | == –Ю–±—А–∞—В–љ–Њ–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ == | ||
| + | |||
| + | –Ю–±—А–∞—В–љ–Њ–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –љ–∞ –±–∞–Ј–µ –њ–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ–і–∞, –±–∞–Ј–Є—А—Г–µ—В—Б—П –љ–∞ –Є–і–µ–µ, —З—В–Њ –ї—О–±–Њ–µ —З–Є—Б–ї–Њ X –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Њ –≤ —Б–Є—Б—В–µ–Љ–µ –≤–Ј–∞–Є–Љ–љ–Њ –њ—А–Њ—Б—В—Л—Е —З–Є—Б–µ–ї <math>p_1,\ldots, p_n</math>, –Ї–∞–Ї [1]: | ||
| + | :<math>X = a_1 + a_2\cdot p_1 + a_3\cdot p_1\cdot p_2 + ... + a_{n-1}\cdot p_1\cdot p_2\cdot \ldots\cdot p_{n-2} + a_n\cdot p_1\cdot p_2\cdot \ldots\cdot p_{n-1}</math>, –≥–і–µ <math>0 < a_i < p_i</math> | ||
| + | * <math>|X|_{p_1} = x_1 = a_1</math> | ||
| + | * <math>|X - a_1|_{p_2} = |x_2 - a_1|_{p_2} = |a_2\cdot p_1|_{p_2}</math> => a<sub>2</sub> = ((p<sub>1</sub><sup>-1</sup>)%p<sub>2</sub>*(x<sub>2</sub> - a<sub>1</sub>))%p<sub>2</sub></li> | ||
| + | <li>(X - a<sub>1</sub> - a<sub>2</sub>*p<sub>1</sub>)%p<sub>3</sub> = (a<sub>3</sub>*p<sub>1</sub>*p<sub>2</sub>)%p<sub>3</sub> => a<sub>3</sub> = ((p<sub>2</sub><sup>-1</sup>)%p<sub>3</sub>*((p<sub>1</sub><sup>-1</sup>)%p<sub>3</sub>*(x<sub>3</sub> - a<sub>1</sub>) - a<sub>2</sub>))%p<sub>3</sub></li> | ||
| + | <li>вА¶</li> | ||
| + | </ul> | ||
| + | –Ф–ї—П –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П —Н—В–Њ–≥–Њ –Љ–µ—В–Њ–і–∞ —В—А–µ–±—Г—О—В—Б—П –Ї–Њ–љ—Б—В–∞–љ—В—Л –≤–Є–і–∞ (p<sub>i</sub><sup>-1</sup>)%p<sub>k</sub><sup>-1</sup>. –Ь–Њ–ґ–љ–Њ —В–∞–Ї–ґ–µ –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –љ–∞—З–Є–љ–∞—В—М –≤—Л—З–Є—Б–ї–µ–љ–Є–µ a<sub>3</sub> –Љ–Њ–ґ–љ–Њ, –Ї–∞–Ї —В–Њ–ї—М–Ї–Њ –њ–Њ—П–≤–Є–ї–Њ—Б—М –Ј–љ–∞—З–µ–љ–Є–µ a<sub>1</sub>. –Э–∞ –Њ—Б–љ–Њ–≤–µ —Н—В–Њ–≥–Њ –Љ–µ—В–Њ–і–∞ –Љ–Њ–ґ–љ–Њ —Б—В—А–Њ–Є—В—М –Ї–Њ–љ–≤–µ–µ—А–љ—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞—В–µ–ї–Є. | ||
| + | |||
| + | == –°—Б—Л–ї–Ї–Є == | ||
| + | [1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York. | ||
–Т–µ—А—Б–Є—П 09:08, 15 –Є—О–ї—П 2013
–Я–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Є–є –Ї–Њ–і (–Є–ї–Є —Б–Є—Б—В–µ–Љ–∞ —Б—З–Є—Б–ї–µ–љ–Є—П —Б–Њ —Б–Љ–µ—И–∞–љ–љ—Л–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ –Њ—В –∞–љ–≥–ї. associated mixed radix system (AMRS))
–Ы—О–±–Њ–µ —З–Є—Б–ї–Њ 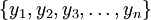 –≤ —Б–Є—Б—В–µ–Љ–µ –Њ—Б—В–∞—В–Њ—З–љ—Л—Е –Ї–ї–∞—Б—Б–Њ–≤ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–љ–Њ –≤ –≤–Є–і–µ –њ–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ–і–∞
–≤ —Б–Є—Б—В–µ–Љ–µ –Њ—Б—В–∞—В–Њ—З–љ—Л—Е –Ї–ї–∞—Б—Б–Њ–≤ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–љ–Њ –≤ –≤–Є–і–µ –њ–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ–і–∞
–≥–і–µ
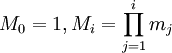 –і–ї—П
–і–ї—П 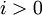 –Є
–Є 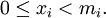
–Я–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Є–є –Ї–Њ–і –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –і–ї—П:
- –°—А–∞–≤–љ–µ–љ–Є—П —З–Є—Б–µ–ї
- –Я–µ—А–µ–≤–Њ–і–∞ —З–Є—Б–µ–ї –Є–Ј —Б–Є—Б—В–µ–Љ—Л –Њ—Б—В–∞—В–Њ—З–љ—Л—Е –Ї–ї–∞—Б—Б–Њ–≤ –≤ –Њ–±—Л—З–љ—Г—О –њ–Њ–Ј–Є—Ж–Є–Њ–љ–љ—Г—О —Б–Є—Б—В–µ–Љ—Г —Б—З–Є—Б–ї–µ–љ–Є—П
–Ю–±—А–∞—В–љ–Њ–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ
–Ю–±—А–∞—В–љ–Њ–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –љ–∞ –±–∞–Ј–µ –њ–Њ–ї–Є–∞–і–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ–і–∞, –±–∞–Ј–Є—А—Г–µ—В—Б—П –љ–∞ –Є–і–µ–µ, —З—В–Њ –ї—О–±–Њ–µ —З–Є—Б–ї–Њ X –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Њ –≤ —Б–Є—Б—В–µ–Љ–µ –≤–Ј–∞–Є–Љ–љ–Њ –њ—А–Њ—Б—В—Л—Е —З–Є—Б–µ–ї 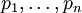 , –Ї–∞–Ї [1]:
, –Ї–∞–Ї [1]:
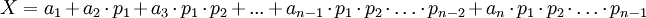 , –≥–і–µ
, –≥–і–µ 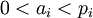
-
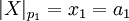
-
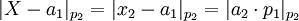 => a2 = ((p1-1)%p2*(x2 - a1))%p2</li>
=> a2 = ((p1-1)%p2*(x2 - a1))%p2</li>
–°—Б—Л–ї–Ї–Є
[1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.