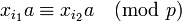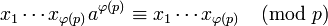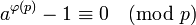Вычисление мультипликативных обратных элементов по заданному модулю
Рассмотрим вопрос о мультипликативных обратных элементов по заданному модулю в фактор-кольце 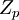 .
.
Теорема
Пусть 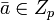 , тогда класс
, тогда класс  имеет мультипликативный обратный элемент по модулю
имеет мультипликативный обратный элемент по модулю  тогда и только тогда, когда
тогда и только тогда, когда 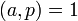 .
.
Теорема
Характеристика 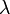 конечного поля – простое число.
конечного поля – простое число.
Рассмотрим два способа вычисления обратных мультипликативных элементов. Первый способ основан на рассмотренном выше алгоритме Евклида, второй – на теореме Эйлера.
Первый способ
Из условия 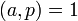 получаем
получаем 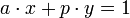 или
или 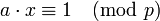 и, следовательно,
и, следовательно, 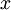 – мультипликативный обратный к
– мультипликативный обратный к  по модулю
по модулю  .
.
Второй способ
Напомним теорему Эйлера.
Определение
Функция Эйлера 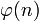 — это количество чисел от
— это количество чисел от 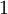 до
до 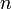 , взаимно простых с
, взаимно простых с 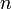 .
.
Т.е. это количество таких натуральных чисел из отрезка ![[1; n]](/w/images/math/e/b/6/eb69e536f0693e0a8cbb9cb04cf98d1d.png) , наибольший общий делитель (НОД) которых с
, наибольший общий делитель (НОД) которых с 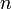 равен единице.
равен единице.
Tеоремa Эйлера
Если  и
и  взаимно просты, то
взаимно просты, то 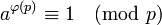 , где
, где 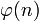 - функция Эйлера.
- функция Эйлера.
Доказательство теоремы достаточно простое, возможны различные варианты. Приведем здесь теоретико-числовое доказательство.
Доказательство
Пусть 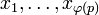 — все различные натуральные числа, меньшие
— все различные натуральные числа, меньшие  и взаимно простые с ним.
и взаимно простые с ним.
Рассмотрим все возможные произведения 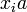 для всех
для всех 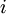 от
от 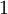 до
до 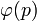 .
.
Поскольку  взаимно просто с
взаимно просто с  и
и 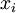 взаимно просто с
взаимно просто с  , то и
, то и 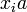 также взаимно просто с
также взаимно просто с  , то есть
, то есть 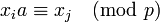 для некоторого
для некоторого 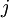 .
.
Отметим, что все остатки 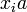 при делении на
при делении на  различны. Действительно, пусть это не так, то существуют такие
различны. Действительно, пусть это не так, то существуют такие 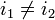 , что
, что
или
-
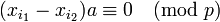 .
.
Так как  взаимно просто с
взаимно просто с  , то последнее равенство равносильно тому, что
, то последнее равенство равносильно тому, что
-
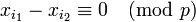 или
или 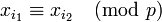 .
.
Это противоречит тому, что числа 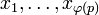 попарно различны по модулю
попарно различны по модулю  .
.
Перемножим все сравнения вида 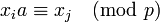 . Получим:
. Получим:
или
-
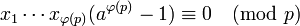 .
.
Так как число 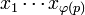 взаимно просто с
взаимно просто с  , то последнее сравнение равносильно тому, что
, то последнее сравнение равносильно тому, что
или
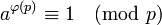 .
.
В частном случае, когда  простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Малая теорема Ферма
Если  - простое число и
- простое число и  - произвольное целое число, не делящееся на
- произвольное целое число, не делящееся на  , то
, то 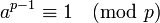 .
.
Следствие
В кольце 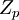 классов вычетов по модулю
классов вычетов по модулю  из
из 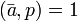 следует, что
следует, что 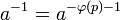 .
.
Таким образом, для вычисления мультипликативного обратного к классу  по модулю
по модулю  в случае, когда
в случае, когда 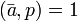 , достаточно
, достаточно  возвести в степень
возвести в степень  , где
, где 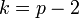 , если
, если  – простое число, и
– простое число, и 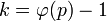 в противном случае.
в противном случае.
При таком методе вычисления мультипликативного обратного элемента задача сводится к цепочке умножений и делений с остатком на модуль  . Эта задача решается без особых трудностей, если наименьший положительный вычет
. Эта задача решается без особых трудностей, если наименьший положительный вычет  , где
, где  , представлен в СОК.
, представлен в СОК.
Однако, вообще говоря, 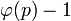 не является наименьшим показателем степени, для которого
не является наименьшим показателем степени, для которого 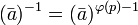 .
.
Разложение кольца вычетов
Из китайской теоремы об остатках следует
Утверждение
Пусть 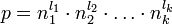 - каноническое представление числа
- каноническое представление числа  . Тогда функция, которая каждому классу
. Тогда функция, которая каждому классу 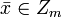 ставит в соответствие кортеж
ставит в соответствие кортеж 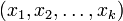 , где
, где 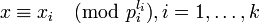 , является кольцевым изоморфизмом кольца
, является кольцевым изоморфизмом кольца 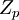 класса вычетов по модулю
класса вычетов по модулю  и кольца кортежей вида
и кольца кортежей вида 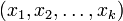 , где
, где 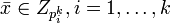 .
.
Более того, если обозначить через 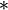 любую из кольцевых операций
любую из кольцевых операций 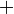 или
или  , то
, то
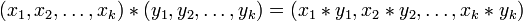 .
.
Таким образом,
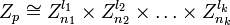 ,
,
т.е. кольцо классов вычетов по модулю  раскладывается в прямое произведение колец классов вычетов по модулям
раскладывается в прямое произведение колец классов вычетов по модулям 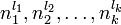 . Это разложение колец индуцирует разложение групп их обратимых элементов:
. Это разложение колец индуцирует разложение групп их обратимых элементов:
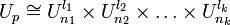 .
.
Можно сделать вывод о том, что произвольное целое положительное число 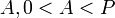 , где
, где 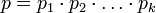 и
и 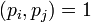 для
для 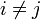 , однозначно представимо своими наименьшими неотрицательными остатками по модулям
, однозначно представимо своими наименьшими неотрицательными остатками по модулям 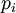 , причём сложение (а, следовательно, и вычитание) и умножение выполняются покомпонентно.
, причём сложение (а, следовательно, и вычитание) и умножение выполняются покомпонентно.