Первообразный корень по модулю
Материал из Модулярная арифметики
Определение
Первообразным (примитивным) корнем по модулю  (от английского primitive root modulo n) называется такое число
(от английского primitive root modulo n) называется такое число 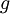 , что все его степени по модулю
, что все его степени по модулю  пробегают по всем числам, взаимно простым с
пробегают по всем числам, взаимно простым с  . Математически это формулируется таким образом: если
. Математически это формулируется таким образом: если 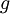 является первообразным корнем по модулю
является первообразным корнем по модулю  , то для любого целого
, то для любого целого  такого, что
такого, что  , найдётся такое целое
, найдётся такое целое 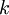 , что
, что 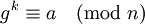 .
.
В частности, для случая простого  степени первообразного корня пробегают по всем числам от
степени первообразного корня пробегают по всем числам от 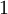 до
до 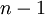 .
.
Существование
Первообразный корень по модулю  существует тогда и только тогда, когда
существует тогда и только тогда, когда  является либо степенью нечётного простого, либо удвоенной степенью простого, а также в случаях
является либо степенью нечётного простого, либо удвоенной степенью простого, а также в случаях 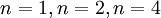 . (Доказано Гауссом в 1801)
. (Доказано Гауссом в 1801)