Результат сравнения модулярных сумматоров в стандартном исполнении и по методу Квайна

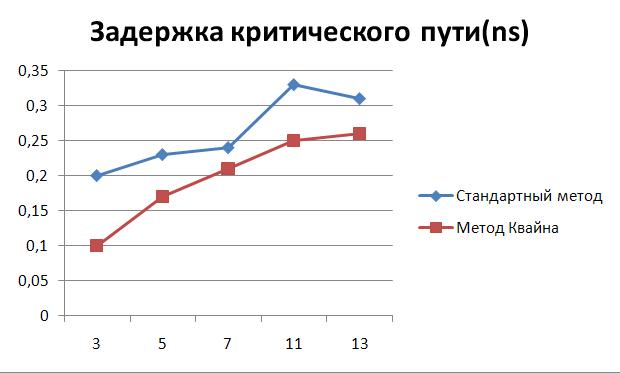
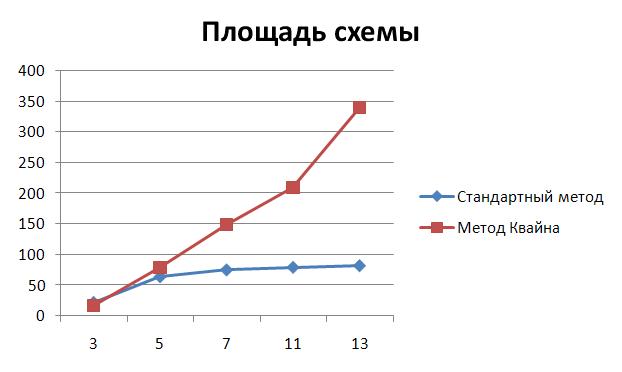
Было произведено сравнение модулярных сумматоров, реализованных на базе стандартных методов и сумматоров, построенных по методу Квайна. Для реализации сумматоров по спец-основаниям вида p=2ⁿ-1 использовались ускоренные комбинационные схемы (Генератор сумматора по модулю 2ⁿ-1). Сравнение производилось для малобитных модулей 3 - 13. Сравнение производилось с помощью САПР Synopsys Design Compiler.

Типовые Verilog-модули

1. Стандартный модулярный сумматор (на примере модуля 11)

// Sum modulo 11
module sum_modulo_11 (A, B, S);
	input [3:0] A;
	input [3:0] B;
	output reg[3:0] S;

		always @(A or B) 
			begin 
					if ({1'b0, A} + {1'b0, B} < 11) S <= {1'b0, A} + {1'b0, B}; 
					else S <= {1'b0, A} + {1'b0, B} - (11); 
			//		else S <= {1'b0, A} + {1'b0, B} + (5); 
			end 
		endmodule 

2. Модулярный сумматор спец вида p=2ⁿ-1 (на примере модуля 7)

// Sum modulo (2^3 - 1) = 7
module sum_modulo_7 (A, B, S);
	input [2:0] A;
	input [2:0] B;
	output[2:0] S;

	wire [2:0] G;
	wire [2:0] P;
	wire [2:0] C;

	assign G[0] = A[0]&B[0];
	assign G[1] = A[1]&B[1];
	assign G[2] = A[2]&B[2];

	assign P[0] = A[0]^B[0];
	assign P[1] = A[1]^B[1];
	assign P[2] = A[2]^B[2];

	assign C[0] = G[0] | G[2]&P[0] | G[1]&P[0]&P[2]; 
	assign C[1] = G[1] | G[0]&P[1] | G[2]&P[1]&P[0]; 
	assign C[2] = G[2] | G[1]&P[2] | G[0]&P[2]&P[1]; 

	assign S[0] = (P[0]&&(~P[2:0]))^C[2];
	assign S[1] = (P[1]&&(~P[2:0]))^C[0];
	assign S[2] = (P[2]&&(~P[2:0]))^C[1];
endmodule

3. Модулярный сумматор по методу Квайна (на примере модуля 7)

// Sum modulo 7
module sum_modulo_7 (A, B, X);
	input [2:0] A;
	input [2:0] B;
	output[2:0] X;

	assign X[0] = (A[0]&~B[0]&~B[1]&~B[2]) | (A[0]&~A[2]&~B[0]&~B[2]) | (A[0]&~A[1]&~A[2]&~B[0]&~B[1]) | (~A[0]&~A[2]&B[0]&~B[2]) 
        | (~A[0]&~A[1]&B[0]&~B[1]&~B[2]) | (~A[0]&~A[1]&~A[2]&B[0]) | (A[1]&A[2]&~B[0]&B[1]) | (A[0]&A[2]&B[0]&B[1]) 
        | (~A[0]&A[2]&~B[0]&B[2]) | (A[0]&A[1]&B[0]&B[2]) | (A[0]&A[2]&B[0]&B[2]) | (~A[0]&A[1]&B[1]&B[2]);
	assign X[1] = (A[1]&~B[0]&~B[1]&~B[2]) | (~A[0]&A[1]&~B[0]&~B[1]) | (~A[0]&A[1]&~A[2]&~B[1]&~B[2]) | (A[0]&~A[1]&B[0]&~B[1]) 
        | (~A[1]&~A[2]&~B[0]&B[1]&~B[2]) | (~A[0]&~A[1]&~B[0]&B[1]) | (~A[0]&~A[1]&~A[2]&B[1]) | (A[0]&A[1]&B[0]&B[1]) 
        | (A[1]&A[2]&B[0]&B[1]) | (A[0]&A[2]&~B[1]&B[2]) | (~A[1]&A[2]&B[0]&B[2]) | (A[0]&A[1]&B[1]&B[2]);
	assign X[2] = (A[2]&~B[0]&~B[1]&~B[2]) | (~A[1]&A[2]&~B[1]&~B[2]) | (~A[0]&~A[1]&A[2]&~B[0]&~B[2]) | (A[0]&A[1]&B[0]&~B[2])
        | (A[1]&~A[2]&B[1]&~B[2]) | (A[0]&~A[2]&B[0]&B[1]) | (~A[1]&~A[2]&~B[1]&B[2]) | (~A[0]&~A[2]&~B[0]&~B[1]&B[2]) 
        | (~A[0]&~A[1]&~A[2]&B[2]) | (A[1]&A[2]&B[0]&B[2]) | (A[0]&A[2]&B[1]&B[2]) | (A[1]&A[2]&B[1]&B[2]);
endmodule

Библиотека стандартных ячеек

NangateOpenCellLibrary_typical_conditional_nldm.lib

Скрипт для запуска

analyze -f verilog <имя модуля>.v
elaborate <имя модуля>
uniquify
current_design <имя модуля>
check_design
set_load [load_of [get_lib_pins NangateOpenCellLibrary/INV_X4/A]] [all_outputs]
set_driving_cell -lib_cell DFFRS_X2 -library NangateOpenCellLibrary -pin Q  [all_inputs] 
set_max_delay -to [all_outputs] 0 
set_max_area 0 
compile
report_timing -significant_digits 6 > timing_<имя модуля>.rpt
report_area > area_<имя модуля>.rpt
report_power -analysis_effort high > power_<имя модуля>.rpt
remove_design -all

Результаты эксперимента

Модули	Стандартный метод		Метод Квайна
	Задержка	Площадь	Задержка	Площадь
3	0.2	22.333	0.1	16.257
5	0.23	63.893	0.17	77.806
7	0.24	74.866	0.21	148.868
11	0.33	79.004	0.25	209.339
13	0.31	81.561	0.26	339.654