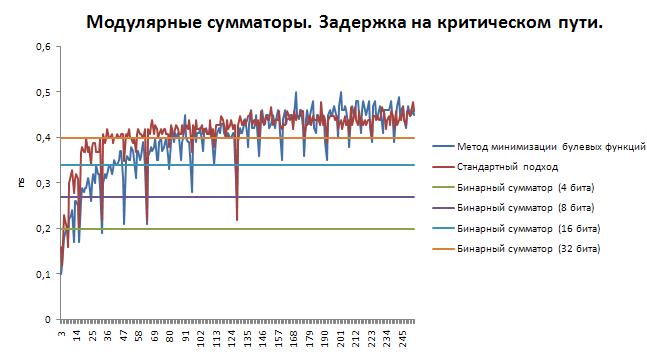
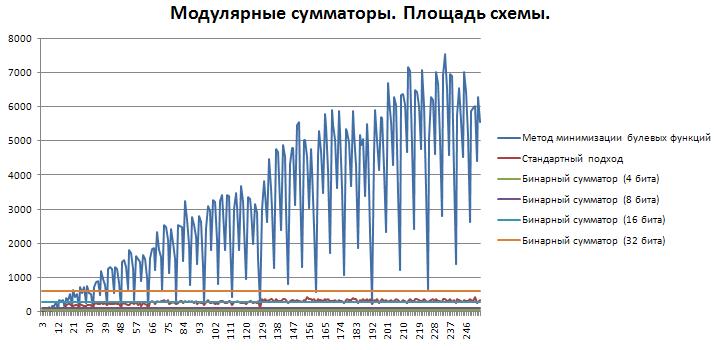
Результат сравнения модулярных сумматоров в стандартном исполнении и по методу Espresso
Было проведено сравнение модулярных сумматоров, реализованных на базе стандартных методов и сумматоров, построенных по методу Espresso. Стандартный метод подразумевает параллельную реализацию суммы двух чисел (a+b), а также суммы сокращенной на модуль (a+b-p). После проверки суммы на выход за диапазон [0,p), выбирается один из вариантов. Метод Espresso заключается в построении таблицы истинности для операции модулярного суммирования, и дальнейшей минимизации получившейся булевой функции методом Espresso. Сравнение проводилось для расширенного набора оснований в диапазоне 3-255, включая числа, не являющиеся простыми. Маршрут проектирования включал минимизацию булевых функций с помощью программного средства Logic Friday. Для автоматизации запуска Logic Friday использовался язык автоматизации AutoIt.
Содержание
Типовые Verilog-модули
1. Стандартный модулярный сумматор (на примере модуля 11)
// Sum modulo 11
module sum_modulo_11 (A, B, S);
input [3:0] A;
input [3:0] B;
output reg[3:0] S;
always @(A or B)
begin
if ({1'b0, A} + {1'b0, B} < 11) S <= {1'b0, A} + {1'b0, B};
else S <= {1'b0, A} + {1'b0, B} - (11);
// else S <= {1'b0, A} + {1'b0, B} + (5);
end
endmodule
2. Модулярный сумматор по методу Espresso (на примере модуля 7)
module adder_mod7 (out, a, b); // Сумматор input [2:0] a, b; output [2:0] out; assign out[2] = (~a[2]&~a[1]&~a[0]&b[2]) | (a[2]&a[1]&b[2]&b[1]) | (a[2]&a[0]&b[2]&b[1]) | (~a[2]&a[1]&~b[2]&b[1]) | (~a[2]&~a[1]&b[2]&~b[1]) | (a[2]&~a[1]&~b[2]&~b[1]) | (a[2]&a[1]&b[2]&b[0]) | (a[1]&a[0]&~b[2]&b[0]) | (~a[2]&a[0]&b[1]&b[0]) | (a[2]&~b[2]&~b[1]&~b[0]) | (a[2]&~a[1]&~a[0]&~b[2]&~b[0]) | (~a[2]&~a[0]&b[2]&~b[1]&~b[0]); assign out[1] = (~a[2]&~a[1]&~a[0]&b[1]) | (a[1]&a[0]&b[2]&b[1]) | (a[2]&a[0]&b[2]&~b[1]) | (a[2]&~a[1]&b[2]&b[0]) | (a[2]&a[1]&b[1]&b[0]) | (a[1]&a[0]&b[1]&b[0]) | (~a[1]&a[0]&~b[1]&b[0]) | (~a[1]&~a[0]&b[1]&~b[0]) | (a[1]&~a[0]&~b[1]&~b[0]) | (a[1]&~b[2]&~b[1]&~b[0]) | (~a[2]&a[1]&~a[0]&~b[2]&~b[1]) | (~a[2]&~a[1]&~b[2]&b[1]&~b[0]); assign out[0] = (a[1]&~a[0]&b[2]&b[1]) | (~a[2]&~a[1]&~a[0]&b[0]) | (a[2]&a[0]&b[2]&b[0]) | (a[1]&a[0]&b[2]&b[0]) | (~a[2]&~a[0]&~b[2]&b[0]) | (a[2]&a[0]&b[1]&b[0]) | (a[2]&~a[0]&b[2]&~b[0]) | (~a[2]&a[0]&~b[2]&~b[0]) | (a[2]&a[1]&b[1]&~b[0]) | (a[0]&~b[2]&~b[1]&~b[0]) | (~a[1]&~a[0]&~b[2]&~b[1]&b[0]) | (~a[2]&~a[1]&a[0]&~b[1]&~b[0]); endmodule
Библиотека стандартных ячеек
NangateOpenCellLibrary.lib
Скрипт для запуска
lappend search_path "../libs" "../src" set target_library "NangateOpenCellLibrary.db" set link_library [list "*" $target_library] analyze -f <имя модуля>.v elaborate <имя модуля> uniquify current_design <имя модуля> check_design set_load [load_of [get_lib_pins NangateOpenCellLibrary/INV_X4/A]] [all_outputs] set_driving_cell -lib_cell DFFRS_X2 -library NangateOpenCellLibrary -pin Q [all_inputs] set_max_delay -to [all_outputs] 0 set_max_area 0 compile report_timing > result/timing_<имя модуля>.rpt report_area > result/area_<имя модуля>.rpt remove_design -all
Файлы для эксперимента
- Несжатые таблицы истинности для сумматоров (.csv, 2MB)
- Сжатые Espresso таблицы истинности для сумматоров (.csv, 3MB)
- Verilog на основе таблиц истинности для сумматоров (.csv, 3MB)
Результаты эксперимента
UPDATE 27.05.13
Было выявлено существенное различие в степени оптимизации различных схем при использовании ULTRA настройки синтезатора. Для более полной картины, все рассматриваемые схемы были синтезированы с ULTRA настройками. Результаты представлены ниже:
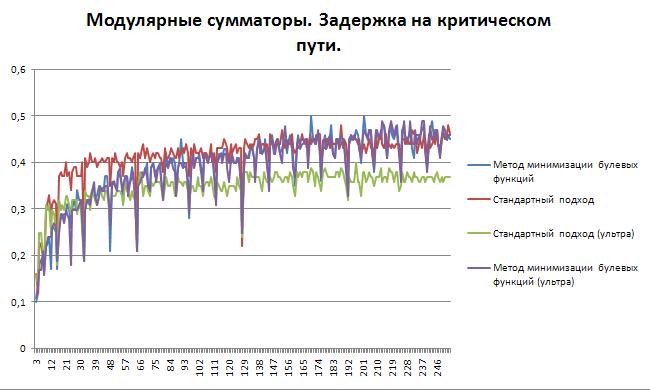
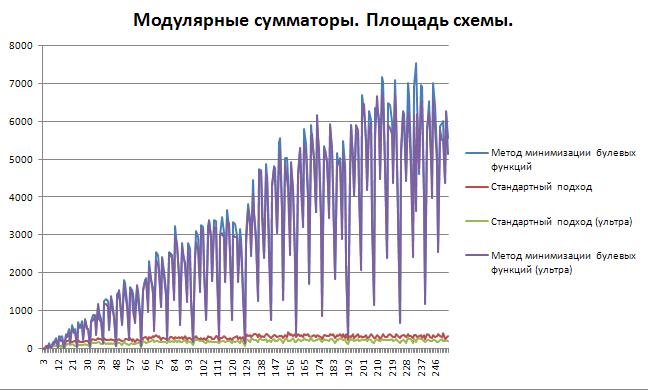
Как можно видеть, более существенные усилия САПР дали выигрыш для стандартного описания сумматоров, и не дали никакого выигрыша для сумматора описанного с помощью булевой функции. Это может объясняться тем, что описывая схему на более высоком уровне абстракции - мы даем синтезатору больше свободы для оптимизации, а описывая схему в виде жестко закрепленных булевых выражений - синтезатор вынужден реализовывать их, и никакие усилия не смогут уменьшить заложенные в это выражение затраты.