Система из 4 модулей (2^n-1, 2^n+1, 2^(n+1)-1, 2^(n+1)+1)
Система модулей {2n-1, 2n+1, 2n+1-1, 2n+1+1} - не является попарно взаимно простой, что несколько сокращает её динамический диапазон, но как будет показано не существенно.
Содержание
Динамический диапазон
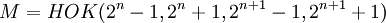
где 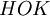 - наименьшее общее кратное.
- наименьшее общее кратное.
Что бы найти 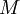 , требуется определить наибольший общий делитель(
, требуется определить наибольший общий делитель(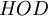 ) для всех четырех модулей. Так как
) для всех четырех модулей. Так как 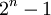 и
и 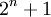 , а также
, а также 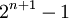 и
и 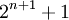 взаимнопросты, то необходимо найти наибольший общий делитель их попарного произведения.
взаимнопросты, то необходимо найти наибольший общий делитель их попарного произведения.
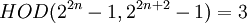
Отсюда по формуле для вычисления 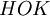 :
:
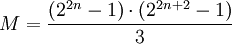
Таблица покрытия
|
n |
Базис |
Покрываемый интервал [0;M) |
Бинарная битность |
|
2 |
3, 5, 7, 9 |
[0; 315) |
8 |
|
3 |
7, 9, 15, 17 |
[0; 5355) |
12 |
|
4 |
15, 17, 31, 33 |
[0; 86955) |
16 |
|
8 |
255, 257, 511, 513 |
[0; 5726513835) |
32 |
|
16 |
65535, 65537, 131071, 131073 |
[0; 24595658757787789995) |
64 |
Прямое преобразование
Для прямого преобразования используются следующие свойства:
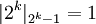 и
и 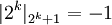
которое позволяет для преобразования целого числа 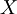 в модулярное представление
в модулярное представление 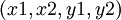 использовать следующие формулы:
использовать следующие формулы:
![x1 = |X[{n-1}:{0}] + X[{2n-1}:{n}] + ... + X[{mn-1}:{(m-1)\cdot n}]|_{2^{n}-1}](/w/images/math/f/0/8/f08606c130d1c869e3ce8cdfc726e751.png)
![x2 = |X[{n-1}:{0}] - X[{2n-1}:{n}] + ... - X[{mn-1}:{(m-1)\cdot n}]|_{2^{n}+1}](/w/images/math/6/f/c/6fcf1249955c80edbb6bbaecfbbb2300.png)
![y1 = |X[{n}:{0}] + X[{2n}:{n+1}] + ... + X[{mn}:{(m-1)\cdot n+1}]|_{2^{n+1}-1}](/w/images/math/1/c/0/1c020e199cc75e3c61465b76077fb757.png)
![y2 = |X[{n}:{0}] - X[{2n}:{n+1}] + ... - X[{mn}:{(m-1)\cdot n+1}]|_{2^{n+1}+1}](/w/images/math/d/f/a/dfad8b49cf23b175da402607e7ed2d55.png)
- Количество слагаемых определяется размерностью входных данных.
- Запись
![X[a:b]](/w/images/math/3/b/c/3bc9fe2ab59084bce63554898b9a1e95.png) - означает взять биты из двоичной записи числа с позиции
- означает взять биты из двоичной записи числа с позиции  до позиции
до позиции  .
.
Так как значение внутри модуля незначительно превосходит сам модуль, то ответ можно получить по следующей схеме:
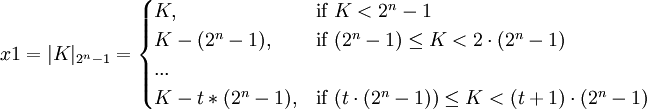
при условии что максимально возможное значение 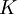 менее чем
менее чем 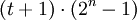
Обратное преобразование
Обратное преобразование строится на базе CRT III (Китайская теорема об остатках ver.3) [1]. Если задана система из двух модулей 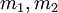 то значение
то значение 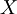 может быть найдено по следующей формуле:
может быть найдено по следующей формуле:
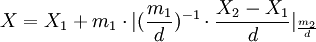
где
-
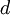 - НОД (наибольший общий делитель)
- НОД (наибольший общий делитель) 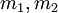
-
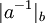 - обратный элемент к
- обратный элемент к  по модулю
по модулю 
- значение
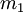 должно быть больше
должно быть больше 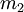
Можно заметить что если 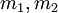 взаимно просты, то
взаимно просты, то 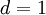 и формула превращается в стандартную формулу полиадического кода (Mixed Radix System).
и формула превращается в стандартную формулу полиадического кода (Mixed Radix System).
Обратный преобразователь для системы модулей из четырех элементов состоит из двух уровней. На первом уровне считаются промежуточные значения 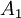 и
и 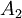 (по формулам CRT III):
(по формулам CRT III):
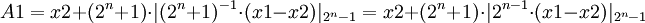
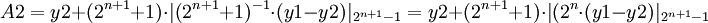
Как видно рассчет обоих коэфициентов легко реализуется на схемном уровне:
- Умножение на
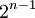 по сути сдвиг
по сути сдвиг
- Умножение
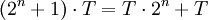 - сдвиг и сложение
- сдвиг и сложение
- Вычет по модулю
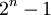 - одно сложение, вычитание и мультиплексор.
- одно сложение, вычитание и мультиплексор.
На втором уровне преобразователя 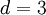 и формула выглядит следующим образом:
и формула выглядит следующим образом:
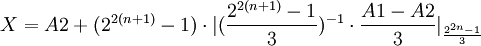
Несложно показать что: 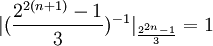 [2]
[2]
Финальная формула в итоге будет:
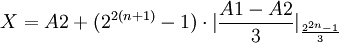
Ссылки
[1] http://etd.lsu.edu/docs/available/etd-11052010-141445/unrestricted/Report_Nov2.pdf