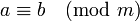Сравнения и их основные свойства
Возьмём произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на
и будем рассматривать остатки при делении на  различных целых чисел.
различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Содержание
Определения
Определение. Два целых числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если их разность
, если их разность 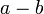 делится без остатка на
делится без остатка на  .
.
Символически сравнимость записывается в виде формулы (сравнения):
Число  называется модулем сравнения.
называется модулем сравнения.
Если разность 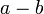 не делится на
не делится на  , то запишем:
, то запишем:
-
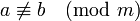 .
.
Согласно определению, 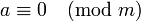 означает, что
означает, что  делится на
делится на  .
.
Теорема.  сравнимо с
сравнимо с  тогда и только тогда, когда
тогда и только тогда, когда  и
и  имеют одинаковые остатки при делении на
имеют одинаковые остатки при делении на  .
Поэтому в качестве определения сравнения можно взять следующую эквивалентную формулировку:
.
Поэтому в качестве определения сравнения можно взять следующую эквивалентную формулировку:
Определение. Целые числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если остатки от деления этих чисел на
, если остатки от деления этих чисел на  равны.
равны.
Примеры
-
 , т. к. 101 – 17 = 84, а 84 делится без остатка на 21.
, т. к. 101 – 17 = 84, а 84 делится без остатка на 21.
-
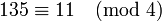 , т. к. оба числа 135 и 11 при делении на 4 дают остаток 3.
, т. к. оба числа 135 и 11 при делении на 4 дают остаток 3.
Свойства
Для фиксированного натурального числа  отношение сравнимости по модулю
отношение сравнимости по модулю  обладает следующими свойствами:
обладает следующими свойствами:
- Рефлексивность: для любого целого
 справедливо
справедливо 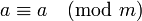 .
.
- Симметричность: если
 , то
, то 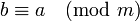 .
.
- Транзитивность: если
 и
и 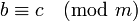 , то
, то 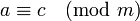 .
.
Таким образом, отношение сравнимости по модулю  является отношением эквивалентности на множестве целых чисел.
является отношением эквивалентности на множестве целых чисел.
- Другие свойства:
- Обе части сравнения можно умножить на произвольное целое число.
- Если
 и
и 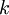 – произвольное целое число, то
– произвольное целое число, то 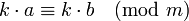 .
.
- Обе части сравнения можно разделить на их общий делитель, если он взаимно прост с модулем.
- Если
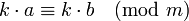 и
и 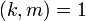 , то
, то  .
.
- Обе части сравнения и модуль можно умножить на одно и то же целое.
- Если
 и
и 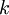 – произвольное натуральное число, то
– произвольное натуральное число, то  .
.
- Обе части сравнения и модуль можно разделить на любой их общий делитель.
- Если
 , где
, где 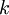 и
и  – произвольные натуральные числа, то
– произвольные натуральные числа, то  .
.
- К любой части сравнения можно прибавить (или отнять от нее) любое число, кратное модуля.
- Если
 то при любом целом
то при любом целом 
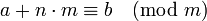 .
.
- Сравнения можно почленно складывать и вычитать.
- Если
 и
и 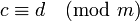 , то
, то 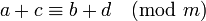 и
и 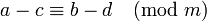 .
.
- Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть.
- Сравнения можно почленно перемножать.
- Если
 и
и 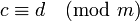 , то
, то 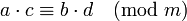 .
.
- Если
 и
и 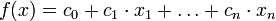 - произвольный многочлен с целыми коэффициентами, то
- произвольный многочлен с целыми коэффициентами, то 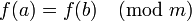 .
.
- Если сравнение выполняется по модулю
 , то оно выполняется и по модулю
, то оно выполняется и по модулю 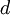 , равному любому делителю числа
, равному любому делителю числа  .
.
- Если
 и
и 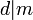 , то
, то 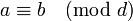 .
.
- Если
 , то множество общих делителей
, то множество общих делителей  и
и  совпадает с множеством общих делителей
совпадает с множеством общих делителей  и
и  . В частности,
. В частности, 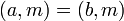 .
.
- Если сравнение
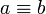 имеет место по нескольким модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
имеет место по нескольким модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
- Если
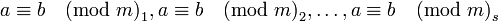 , то
, то  , где
, где ![m = [m_1, m_2, \ldots, m_s]](/w/images/math/9/1/c/91cfa423b902ea14a3811c08c0bd6d0d.png) .
.
- Если одна часть сравнения и модуль делятся на какое-либо число, то и другая часть сравнения делится на это число.
Классы вычетов
При делении целых чисел на модуль  в остатке получатся числа
в остатке получатся числа 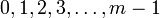 .
.
Отнесём все целые числа, дающие при делении на  один и тот же остаток в один класс, поэтому получится
один и тот же остаток в один класс, поэтому получится  различных классов по модулю
различных классов по модулю  . В один класс попадут равноостаточные числа, они называются вычетами друг друга.
. В один класс попадут равноостаточные числа, они называются вычетами друг друга.
Определение. Множество всех чисел сравнимых с  по модулю
по модулю  называется классом вычетов
называется классом вычетов  по модулю
по модулю  .
.
Обозначим через 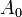 класс вычетов, которые при делении на
класс вычетов, которые при делении на  дают остаток
дают остаток 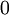 .
.
Например, числа вида 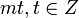 .
.
Через 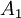 – числа, дающие при делении остаток
– числа, дающие при делении остаток 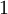 .
.
Например, числа вида 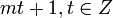 .
.
Через 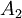 – числа, дающие при делении остаток
– числа, дающие при делении остаток 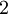 .
.
Например, числа вида 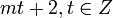 .
.
Через 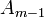 – числа, дающие при делении остаток
– числа, дающие при делении остаток 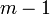 .
.
Например, числа вида 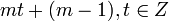 .
.
Определение. Полной системой вычетов по модулю  называется совокупность
называется совокупность  целых чисел, содержащая точно по одному представителю из каждого класса вычетов по модулю
целых чисел, содержащая точно по одному представителю из каждого класса вычетов по модулю  .
.
Каждый класс вычетов по модулю  содержит в точности одно из чисел совокупности всех возможных остатков от деления на
содержит в точности одно из чисел совокупности всех возможных остатков от деления на  :
: 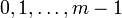 .
.
Можно доказать, что любая совокупность  чисел
чисел 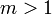 , попарно несравнимых по модулю
, попарно несравнимых по модулю  , есть полная система вычетов по модулю
, есть полная система вычетов по модулю  .
.
Часто рассматривают полную систему наименьших неотрицательных вычетов по модулю  :
:
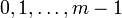 ;
;
полную систему наименьших положительных вычетов:
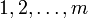 ;
;
полную систему наименьших по абсолютной величине вычетов:
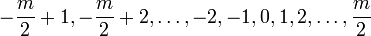 при чётном
при чётном  ;
;
![-\left[{\frac{m}{2}}\right], {-\left[{\frac{m}{2}}\right]+1}, \ldots, -2, -1, 0, 1, 2, \ldots, \left[{\frac{m}{2}}\right]](/w/images/math/8/7/1/871bcfd5b12caed022e91d247a8e6a88.png) при нечётном
при нечётном  .
.
Определение. Приведенной системой вычетов по модулю m называется совокупность всех вычетов из полной системы, взаимно простых с модулем  .
.
Иначе говоря, приведённая система вычетов по модулю  - это система чисел, взаимно простых с модулем, взятых по одному и только по одному из каждого класса вычетов по модулю
- это система чисел, взаимно простых с модулем, взятых по одному и только по одному из каждого класса вычетов по модулю  . Приведенную систему обычно выбирают из системы наименьших неотрицательных вычетов. Число классов, взаимно простых с модулем
. Приведенную систему обычно выбирают из системы наименьших неотрицательных вычетов. Число классов, взаимно простых с модулем  , равно значению функции Эйлера
, равно значению функции Эйлера 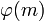 .
.