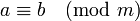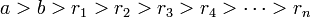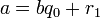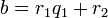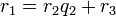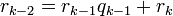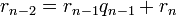Система остаточных классов - введение — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 4: | Строка 4: | ||
| − | Определение | + | '''Определение''' |
| + | |||
| + | Говорят, что целое число <math>n</math> делится на натуральное число <math>m</math> с остатком, если имеется пара целых чисел <math>q</math> и <math>r</math>, таких, что <math>n = m \cdot q+r</math> и <math>0\le r<m</math>. | ||
<math>n</math> называется делимым, <math>m</math> - делителем, <math>q</math> - неполным частным, <math>r</math> - остатком. | <math>n</math> называется делимым, <math>m</math> - делителем, <math>q</math> - неполным частным, <math>r</math> - остатком. | ||
| + | |||
Для целых чисел: | Для целых чисел: | ||
| − | |||
| + | '''Определение''' | ||
| + | |||
| + | Говорят, что целое число <math>n \in Z</math> делится на натуральное число <math>m \in Z</math> с остатком, если имеется пара целых чисел <math>q</math> и <math>r</math>, таких, что <math>n = m \cdot q+r</math> и <math>0\le r<|m|</math>. | ||
| + | |||
| + | |||
| + | '''Пример''': | ||
| − | + | '''48''' при делении на '''5''' даёт остаток '''3''', т.к. <math>48=5\cdot 9+3</math>, <math>0\le 3<5</math>, '''-48''' при делении на '''5''' даёт остаток '''2''', т.к. <math>-48=5\cdot (-10)+2</math>, <math>0\le 2<5</math>. | |
| Строка 21: | Строка 29: | ||
| − | Определение | + | '''Определение''' |
| + | |||
| + | Два целых числа <math> a </math> и <math> b </math> называются '''сравнимыми по модулю <math> m </math>''', если их разность <math> a-b </math> делится без остатка на <math> m </math>. | ||
| + | |||
Символически сравнимость записывается в виде формулы ('''сравнения'''): | Символически сравнимость записывается в виде формулы ('''сравнения'''): | ||
| + | |||
: <math>a \equiv b \pmod{m}</math> | : <math>a \equiv b \pmod{m}</math> | ||
| Строка 30: | Строка 42: | ||
Эквивалентная формулировка: | Эквивалентная формулировка: | ||
| − | Определение | + | '''Определение''' |
| + | |||
| + | Целые числа <math> a </math> и <math> b </math> называются '''сравнимыми по модулю <math> m </math>''', если остатки от деления этих чисел на <math> m </math> равны. | ||
| + | |||
Отношение сравнимости по модулю <math> m </math> обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности. | Отношение сравнимости по модулю <math> m </math> обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности. | ||
| Строка 42: | Строка 57: | ||
'''Теорема о делении с остатком''' | '''Теорема о делении с остатком''' | ||
| − | + | ||
| − | <math>b \not= 0</math>, существует единственный набор целых чисел ''q'' и ''r'', что a = bq + r и <math>0 \le r < |b|</math>, где |''b''| — модуль числа ''b''. | + | Для любых целых ''a'' и ''b'', <math>b \not= 0</math>, существует единственный набор целых чисел ''q'' и ''r'', что a = bq + r и <math>0 \le r < |b|</math>, где |''b''| — модуль числа ''b''. |
| + | |||
На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел. | На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел. | ||
| Строка 65: | Строка 81: | ||
Тогда НОД(''a'',''b''), наибольший общий делитель <math>a</math> и <math>b</math>, равен | Тогда НОД(''a'',''b''), наибольший общий делитель <math>a</math> и <math>b</math>, равен | ||
<math>r_n</math>, последнему ненулевому члену этой последовательности. | <math>r_n</math>, последнему ненулевому члену этой последовательности. | ||
| + | |||
'''Существование''' таких <math>r_1, r_2, ...</math>, то есть возможность деления с остатком <math>a</math> на <math>b</math> для любого целого <math>a</math> и целого <math>b\ne 0</math>, доказывается индукцией. | '''Существование''' таких <math>r_1, r_2, ...</math>, то есть возможность деления с остатком <math>a</math> на <math>b</math> для любого целого <math>a</math> и целого <math>b\ne 0</math>, доказывается индукцией. | ||
'''Корректность''' этого алгоритма вытекает из следующих двух утверждений: | '''Корректность''' этого алгоритма вытекает из следующих двух утверждений: | ||
| + | |||
* Пусть <math>a = bq + r</math>, тогда НОД (<math>a</math>, <math>b</math>) = НОД (<math>b</math>, <math>r</math>). | * Пусть <math>a = bq + r</math>, тогда НОД (<math>a</math>, <math>b</math>) = НОД (<math>b</math>, <math>r</math>). | ||
* НОД(0,<math>r</math>) = <math>r</math> для любого ненулевого <math>r</math> (так как 0 делится на любое целое число, кроме нуля). | * НОД(0,<math>r</math>) = <math>r</math> для любого ненулевого <math>r</math> (так как 0 делится на любое целое число, кроме нуля). | ||
| Строка 82: | Строка 100: | ||
В современной формулировке теорема звучит так: | В современной формулировке теорема звучит так: | ||
| − | Теорема | + | '''Теорема''' |
Пусть <math>p_1, p_2, \ldots, p_k</math> - попарно взаимно простые числа, большие 1, и пусть <math>p = p_1 \cdot p_2 \cdot \ldots \cdot p_k</math>. Тогда существует единственное неотрицательное решение по модулю <math>p</math> следующей системы сравнений: | Пусть <math>p_1, p_2, \ldots, p_k</math> - попарно взаимно простые числа, большие 1, и пусть <math>p = p_1 \cdot p_2 \cdot \ldots \cdot p_k</math>. Тогда существует единственное неотрицательное решение по модулю <math>p</math> следующей системы сравнений: | ||
| Строка 89: | Строка 107: | ||
: <math>\ldots</math>, | : <math>\ldots</math>, | ||
: <math>x \equiv a_k \pmod{p_k}</math>. | : <math>x \equiv a_k \pmod{p_k}</math>. | ||
| + | |||
Другими словами, отображение, которое каждому целому числу <math>x</math>, <math>0\le x <p</math>, ставит в соответствие кортеж <math>a_1, a_2,\ldots, a_k</math>, где <math>x \equiv a_i \pmod{p_i}, i = 1, \ldots k</math> является биекцией кольца <math>Z_P</math> на декартово произведение <math>Z_{p_1} \times Z_{p_2} \times \ldots \times Z_{p_k}</math> колец <math>Z_{p_1}, Z_{p_2}, \ldots, Z_{p_k}</math>. | Другими словами, отображение, которое каждому целому числу <math>x</math>, <math>0\le x <p</math>, ставит в соответствие кортеж <math>a_1, a_2,\ldots, a_k</math>, где <math>x \equiv a_i \pmod{p_i}, i = 1, \ldots k</math> является биекцией кольца <math>Z_P</math> на декартово произведение <math>Z_{p_1} \times Z_{p_2} \times \ldots \times Z_{p_k}</math> колец <math>Z_{p_1}, Z_{p_2}, \ldots, Z_{p_k}</math>. | ||
| Строка 97: | Строка 116: | ||
== Теоремы Эйлера и Ферма, их роль в вычислении мультипликативных обратных элементов по заданному модулю == | == Теоремы Эйлера и Ферма, их роль в вычислении мультипликативных обратных элементов по заданному модулю == | ||
| + | |||
| + | '''Определение''' | ||
| + | |||
| + | Функция Эйлера <math>phi (n)</math> — это количество чисел от <math>1</math> до <math>n</math>, взаимно простых с <math>n</math>. | ||
| + | |||
| + | |||
| + | Т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с <math>n</math> равен единице. | ||
| + | |||
| + | |||
| + | '''Tеоремa Эйлера''' | ||
| + | |||
| + | Если <math>a</math> и <math>p</math> взаимно просты, то <math>a^{phi(p)} \equiv 1 \pmod p</math>, где <math>phi (n)</math> - функция Эйлера. | ||
| + | |||
| + | |||
| + | В частном случае, когда <math>m</math> простое, теорема Эйлера превращается в так называемую малую теорему Ферма: | ||
| + | Частным случаем теоремы Эйлера является малая теорема Ферма. | ||
| + | |||
| + | |||
| + | '''Малая теорема Ферма''' | ||
| + | |||
| + | Если <math>p</math> - простое число и <math>a</math> - произвольное целое число, не делящееся на <math>p</math>, то <math>a^{p-1} \equiv 1 \pmod p </math>. | ||
| + | |||
| + | |||
| + | Смотри [[Функция Эйлера|Функция Эйлера]], [[Вычисление мультипликативных обратных элементов по заданному модулю][Вычисление мультипликативных обратных элементов по заданному модулю]]. | ||
| + | |||
== Числа Мерсенна, Ферма и операции над ними == | == Числа Мерсенна, Ферма и операции над ними == | ||
Версия 16:54, 4 сентября 2014
Содержание
Теоретико-числовая база построения системы остаточных классов
Напомним определение деления с остатком.
Определение
Говорят, что целое число 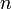 делится на натуральное число
делится на натуральное число  с остатком, если имеется пара целых чисел
с остатком, если имеется пара целых чисел 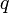 и
и  , таких, что
, таких, что 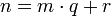 и
и 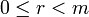 .
.
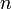 называется делимым,
называется делимым,  - делителем,
- делителем, 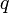 - неполным частным,
- неполным частным,  - остатком.
- остатком.
Для целых чисел:
Определение
Говорят, что целое число 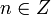 делится на натуральное число
делится на натуральное число 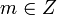 с остатком, если имеется пара целых чисел
с остатком, если имеется пара целых чисел 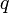 и
и  , таких, что
, таких, что 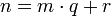 и
и 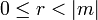 .
.
Пример:
48 при делении на 5 даёт остаток 3, т.к. 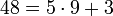 ,
, 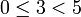 , -48 при делении на 5 даёт остаток 2, т.к.
, -48 при делении на 5 даёт остаток 2, т.к. 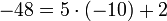 ,
, 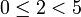 .
.
Сравнения и их основные свойства
Возьмём произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на
и будем рассматривать остатки при делении на  различных целых чисел.
различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Определение
Два целых числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если их разность
, если их разность 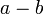 делится без остатка на
делится без остатка на  .
.
Символически сравнимость записывается в виде формулы (сравнения):
Число  называется модулем сравнения.
называется модулем сравнения.
Эквивалентная формулировка:
Определение
Целые числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если остатки от деления этих чисел на
, если остатки от деления этих чисел на  равны.
равны.
Отношение сравнимости по модулю  обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
Отнесём все целые числа, дающие при делении на  один и тот же остаток в один класс, поэтому получится
один и тот же остаток в один класс, поэтому получится  различных классов по модулю
различных классов по модулю  .
Множество всех чисел сравнимых с
.
Множество всех чисел сравнимых с  по модулю
по модулю  называется классом вычетов
называется классом вычетов  по модулю
по модулю  .
.
Подробнее о свойствах сравнений и классах вычетов смотри Сравнения и их основные свойства
Теорема о делении с остатком. Алгоритм Евклида
Теорема о делении с остатком
Для любых целых a и b, 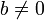 , существует единственный набор целых чисел q и r, что a = bq + r и
, существует единственный набор целых чисел q и r, что a = bq + r и 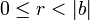 , где |b| — модуль числа b.
, где |b| — модуль числа b.
На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.
Алгоритм Евклида для целых чисел
Пусть  и
и  — целые числа, не равные одновременно нулю, и последовательность чисел
— целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое 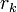 — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
— это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
Тогда НОД(a,b), наибольший общий делитель  и
и  , равен
, равен
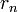 , последнему ненулевому члену этой последовательности.
, последнему ненулевому члену этой последовательности.
Существование таких 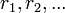 , то есть возможность деления с остатком
, то есть возможность деления с остатком  на
на  для любого целого
для любого целого  и целого
и целого 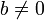 , доказывается индукцией.
, доказывается индукцией.
Корректность этого алгоритма вытекает из следующих двух утверждений:
- Пусть
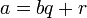 , тогда НОД (
, тогда НОД ( ,
,  ) = НОД (
) = НОД ( ,
,  ).
).
- НОД(0,
 ) =
) =  для любого ненулевого
для любого ненулевого  (так как 0 делится на любое целое число, кроме нуля).
(так как 0 делится на любое целое число, кроме нуля).
Китайская теорема об остатках
Фундаментальным положением, лежащим в основе модулярного представления чисел, является китайская теорема об остатках (Chinese Remainder Theorem - CRT). Например, эта теорема гарантирует, что при правильном выборе модулей СОК каждое число из динамического диапазона имеет в СОК единственное представление, и по этому представлению можно определить представленное число. В своей первоначальной формулировке эта теорема была доказана китайским математиком Сунь-Цзы приблизительно в 100 г. н.э. В современной формулировке теорема звучит так:
Теорема
Пусть 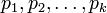 - попарно взаимно простые числа, большие 1, и пусть
- попарно взаимно простые числа, большие 1, и пусть 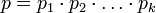 . Тогда существует единственное неотрицательное решение по модулю
. Тогда существует единственное неотрицательное решение по модулю  следующей системы сравнений:
следующей системы сравнений:
-
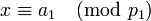 ,
,
-
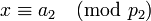 ,
,
-
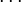 ,
,
-
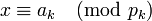 .
.
Другими словами, отображение, которое каждому целому числу 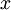 ,
, 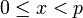 , ставит в соответствие кортеж
, ставит в соответствие кортеж 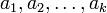 , где
, где 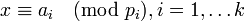 является биекцией кольца
является биекцией кольца 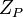 на декартово произведение
на декартово произведение 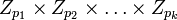 колец
колец 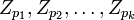 .
.
Подробности и доказательство теоремы смотри Китайская теорема об остатках.
Смотри также Китайская теорема об остатках(КТО II), Китайская теорема об остатках (КТО III).
Теоремы Эйлера и Ферма, их роль в вычислении мультипликативных обратных элементов по заданному модулю
Определение
Функция Эйлера 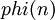 — это количество чисел от
— это количество чисел от 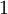 до
до 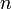 , взаимно простых с
, взаимно простых с 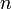 .
.
Т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с 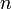 равен единице.
равен единице.
Tеоремa Эйлера
Если  и
и  взаимно просты, то
взаимно просты, то 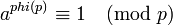 , где
, где 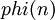 - функция Эйлера.
- функция Эйлера.
В частном случае, когда  простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Частным случаем теоремы Эйлера является малая теорема Ферма.
простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Частным случаем теоремы Эйлера является малая теорема Ферма.
Малая теорема Ферма
Если  - простое число и
- простое число и  - произвольное целое число, не делящееся на
- произвольное целое число, не делящееся на  , то
, то 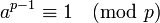 .
.
Смотри Функция Эйлера, [[Вычисление мультипликативных обратных элементов по заданному модулю][Вычисление мультипликативных обратных элементов по заданному модулю]].