Комплексное исследование обратных преобразователей — различия между версиями

Материал из Модулярная арифметики
Перейти к: навигация, поиск
(Новая страница: «== Описание эксперимента == Было проведено исследование универсальных обратных преобраз…»)
 
 
(не показано 8 промежуточных версии этого же участника)
Строка 72: Строка 72:
 
}
 
}
 
</pre>
 
</pre>
 +
 +
== Результаты ==
 +
 +
=== Модули (3 5 7) ===
 +
* Дефолтный тест с малыми модулями
 +
<table cellpadding=5 cellspacing=0 border=1>
 +
<tr>
 +
<td>Метод</td>
 +
<td>Задержка</td>
 +
<td>Общая латентность</td>
 +
<td>Площадь</td>
 +
<td>Мощность</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Комбинационная</td>
 +
<td>1.657336</td>
 +
<td>1.657336</td>
 +
<td>588 </td>
 +
<td>0.454</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Конвеерная</td>
 +
<td>1.03069</td>
 +
<td>2.06138</td>
 +
<td>678 </td>
 +
<td>0.493</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический c LUT</td>
 +
<td>0.408523</td>
 +
<td>1.225569</td>
 +
<td>468 </td>
 +
<td>2.3425</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический без таблиц LUT</td>
 +
<td>0.694463</td>
 +
<td>2.083389</td>
 +
<td>507 </td>
 +
<td>3.1857</td>
 +
</tr>
 +
</table>
 +
 +
=== Модули (193 257 449) ===
 +
* Типовые модули для небольшого модулярного FIR-фильтра
 +
<table cellpadding=5 cellspacing=0 border=1>
 +
<tr>
 +
<td>Метод</td>
 +
<td>Задержка</td>
 +
<td>Общая латентность</td>
 +
<td>Площадь</td>
 +
<td>Мощность</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Комбинационная</td>
 +
<td>4.360145</td>
 +
<td>4.360145</td>
 +
<td>4162 </td>
 +
<td>5.1871</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Конвеерная</td>
 +
<td>3.181364</td>
 +
<td>6.362728</td>
 +
<td>4317 </td>
 +
<td>37</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический c LUT</td>
 +
<td>1.034454</td>
 +
<td>3.103362</td>
 +
<td>81678 </td>
 +
<td>107</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический без таблиц LUT</td>
 +
<td>2.091278</td>
 +
<td>6.273834</td>
 +
<td>3213 </td>
 +
<td>27</td>
 +
</tr>
 +
</table>
 +
 +
=== Модули (3 5 7 11 13 17 23 31) ===
 +
* Много модулей малой разрядности
 +
<table cellpadding=5 cellspacing=0 border=1>
 +
<tr>
 +
<td>Метод</td>
 +
<td>Задержка</td>
 +
<td>Общая латентность</td>
 +
<td>Площадь</td>
 +
<td>Мощность</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Комбинационная</td>
 +
<td>7.564148</td>
 +
<td>7.564148</td>
 +
<td>8765 </td>
 +
<td>11</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Конвеерная</td>
 +
<td>3.961807</td>
 +
<td>11.885421</td>
 +
<td>8154 </td>
 +
<td>71</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический c LUT</td>
 +
<td>0.669079</td>
 +
<td>5.352632</td>
 +
<td>12919</td>
 +
<td>70</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический без таблиц LUT</td>
 +
<td>1.674882</td>
 +
<td>13.399056</td>
 +
<td>7969</td>
 +
<td>69</td>
 +
</tr>
 +
</table>
 +
 +
=== Модули (511 512 513) ===
 +
* Специальная система модулей вида (2<sup>n</sup>-1, 2<sup>n</sup>, 2<sup>n</sup>+1)
 +
<table cellpadding=5 cellspacing=0 border=1>
 +
<tr>
 +
<td>Метод</td>
 +
<td>Задержка</td>
 +
<td>Общая латентность</td>
 +
<td>Площадь</td>
 +
<td>Мощность</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Комбинационная</td>
 +
<td>3.584309</td>
 +
<td>3.584309</td>
 +
<td>3049 </td>
 +
<td>2.6</td>
 +
</tr>
 +
<tr>
 +
<td>CRT 2 Конвеерная</td>
 +
<td>2.404739</td>
 +
<td>7.214217</td>
 +
<td>3160 </td>
 +
<td>21</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический c LUT</td>
 +
<td>1.05807</td>
 +
<td>3.17421</td>
 +
<td>155055</td>
 +
<td>139</td>
 +
</tr>
 +
<tr>
 +
<td>Полиадический без таблиц LUT</td>
 +
<td>2.445659</td>
 +
<td>7.336977</td>
 +
<td>3849</td>
 +
<td>26</td>
 +
</tr>
 +
<tr>
 +
<td>Специализированный преобразователь</td>
 +
<td>0.82</td>
 +
<td>0.82</td>
 +
<td>1696</td>
 +
<td>---</td>
 +
</tr>
 +
</table>
 +
 +
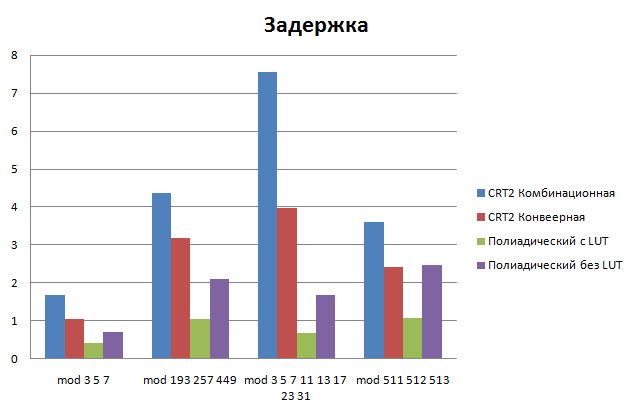
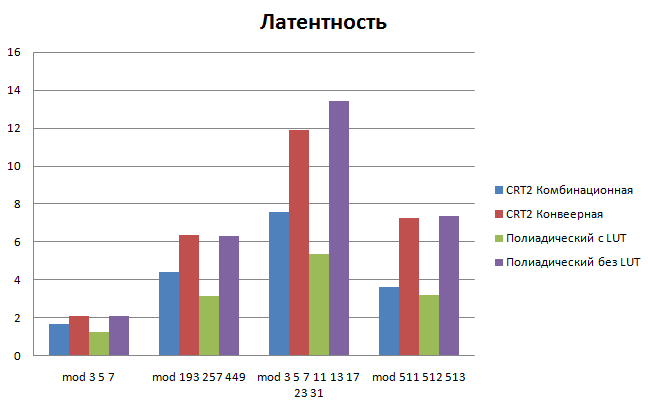
[[Изображение:Комплексное исследование обратных преобразователей-Задержка.png]] [[Изображение:Комплексное исследование обратных преобразователей-Латентность.png]]
 +
 +
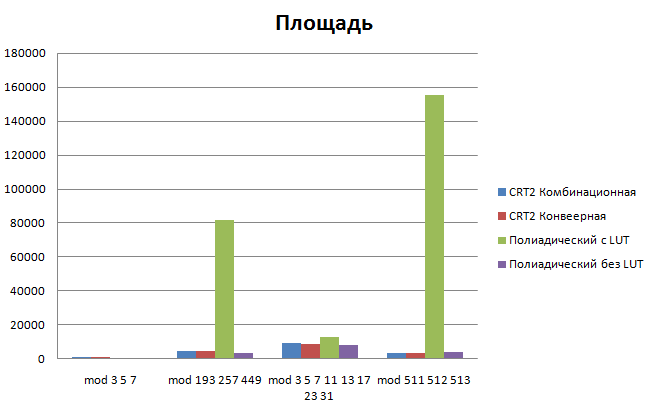
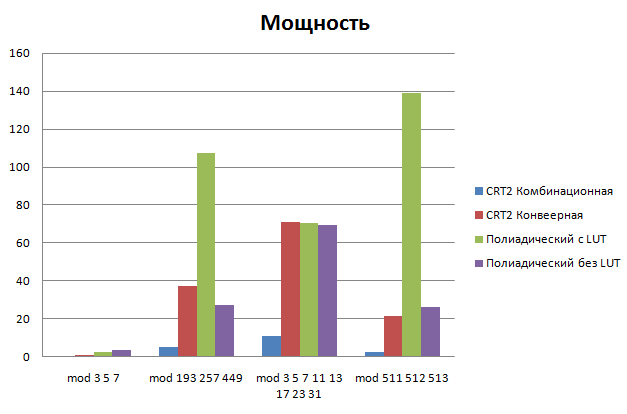
[[Изображение:Комплексное исследование обратных преобразователей-Площадь.png]] [[Изображение:Комплексное исследование обратных преобразователей-Мощность.png]]
  
 
== Выводы ==
 
== Выводы ==
 +
* Наиболее быстрым методом является "Полиадический с LUT (таблицами)", однако он является применимым лишь в случаях, когда используемые модули имеют маленькие значение. Иначе сильно растет площадь и мощность устройства.
 +
* Площадь всех остальных методов примерно одинакова и растет незначительно в зависимости от размера задачи
 +
* Мощность комбинационной версии является минимальной.
 +
* В случае когда требуется максимальная частота преобразователя, логично использовать полиадический преобразователь
 +
* В случае когда требуется минимальная латентность лучше использовать комбинационный преобразователь на базе CRT II
 +
* Если для задачи есть специализированный преобразователь (см. таблицу 511 512 513), то логично использовать именно его.
 +
* Похоже есть возможность разбить Конвеерный преобразователь на базе CRT II, на большее число этапов и тем самым повысить его эффективность. В данный момент задержка определяется последним этапом алгоритма CRT II, где сходятся максимальные модули. В итоге увеличивается общая латентность схемы и уменьшается возможная тактовая частота.
  
 
== Файлы с входными данными ==
 
== Файлы с входными данными ==
 +
* [http://vscripts.ru/res/files/2013_08_reverse_converters_test_verilog.zip Verilog (zip)]
  
 
== Файл с результатами ==
 
== Файл с результатами ==
 +
* [http://vscripts.ru/res/files/2013_08_reverse_converters_test_verilog.zip Результаты модулирования (zip)]
 +
* [http://vscripts.ru/res/files/2013_08_reverse_converters_test_results.xlsx Excel-таблица со сводными результатами]

Текущая версия на 12:18, 21 августа 2013

Описание эксперимента

Было проведено исследование универсальных обратных преобразователей (для произвольных систем модулей). Для тестирования использовались следующие подходы:

Исследовались задержка и площадь. Также для спец. систем модулей сравнивались параметры со специализированными конвертерами.

Библиотека стандартных ячеек

NangateOpenCellLibrary.lib

Скрипт для запуска

set seq_run {"poilad-lut-511-512-513" "poilad-511-512-513" "seq-511-512-513"}
set comb_run {"comb-511-512-513"}

foreach design $comb_run {

	lappend search_path "../libs" "../src" "./verilog" "./"
	set target_library "NangateOpenCellLibrary.db"
	set link_library [list "*" $target_library]

	analyze -format verilog $design.v

	elaborate reverse_conv
	uniquify
	current_design reverse_conv
	check_design
	set_load [load_of [get_lib_pins NangateOpenCellLibrary/INV_X4/A]] [all_outputs]
	set_driving_cell -lib_cell DFFRS_X2 -library NangateOpenCellLibrary -pin Q  [all_inputs] 
	set_max_delay -to [all_outputs] 0 
	set_max_area 0 
	compile
	report_timing -significant_digits 6 -max_paths 10 > "timing.$design.rpt"
	report_area > "area.$design.rpt"
	report_power -analysis_effort high > "power.$design.rpt"

	remove_design -all
}

#with_clock
foreach design $seq_run {

	lappend search_path "../libs" "../src" "./verilog" "./"
	set target_library "NangateOpenCellLibrary.db"
	set link_library [list "*" $target_library]

	analyze -format verilog $design.v

	elaborate reverse_conv
	uniquify
	current_design reverse_conv
	check_design
	set_load [load_of [get_lib_pins NangateOpenCellLibrary/INV_X4/A]] [all_outputs]
	set_driving_cell -lib_cell DFFRS_X2 -library NangateOpenCellLibrary -pin Q  [all_inputs] 
	set_max_delay -to [all_outputs] 0 
	set_max_area 0 
	create_clock clk -period 0.1
	set_clock_uncertainty 0.0 [all_clocks]
	set_dont_touch_network [all_clocks]
	compile
	report_timing -significant_digits 6 -max_paths 10 > "timing.$design.rpt"
	report_area > "area.$design.rpt"
	report_power -analysis_effort high > "power.$design.rpt"

	remove_design -all
}

Результаты

Модули (3 5 7)

  • Дефолтный тест с малыми модулями
Метод Задержка Общая латентность Площадь Мощность
CRT 2 Комбинационная 1.657336 1.657336 588 0.454
CRT 2 Конвеерная 1.03069 2.06138 678 0.493
Полиадический c LUT 0.408523 1.225569 468 2.3425
Полиадический без таблиц LUT 0.694463 2.083389 507 3.1857

Модули (193 257 449)

  • Типовые модули для небольшого модулярного FIR-фильтра
Метод Задержка Общая латентность Площадь Мощность
CRT 2 Комбинационная 4.360145 4.360145 4162 5.1871
CRT 2 Конвеерная 3.181364 6.362728 4317 37
Полиадический c LUT 1.034454 3.103362 81678 107
Полиадический без таблиц LUT 2.091278 6.273834 3213 27

Модули (3 5 7 11 13 17 23 31)

  • Много модулей малой разрядности
Метод Задержка Общая латентность Площадь Мощность
CRT 2 Комбинационная 7.564148 7.564148 8765 11
CRT 2 Конвеерная 3.961807 11.885421 8154 71
Полиадический c LUT 0.669079 5.352632 12919 70
Полиадический без таблиц LUT 1.674882 13.399056 7969 69

Модули (511 512 513)

  • Специальная система модулей вида (2n-1, 2n, 2n+1)
Метод Задержка Общая латентность Площадь Мощность
CRT 2 Комбинационная 3.584309 3.584309 3049 2.6
CRT 2 Конвеерная 2.404739 7.214217 3160 21
Полиадический c LUT 1.05807 3.17421 155055 139
Полиадический без таблиц LUT 2.445659 7.336977 3849 26
Специализированный преобразователь 0.82 0.82 1696 ---

Комплексное исследование обратных преобразователей-Задержка.png Комплексное исследование обратных преобразователей-Латентность.png

Комплексное исследование обратных преобразователей-Площадь.png Комплексное исследование обратных преобразователей-Мощность.png

Выводы

  • Наиболее быстрым методом является "Полиадический с LUT (таблицами)", однако он является применимым лишь в случаях, когда используемые модули имеют маленькие значение. Иначе сильно растет площадь и мощность устройства.
  • Площадь всех остальных методов примерно одинакова и растет незначительно в зависимости от размера задачи
  • Мощность комбинационной версии является минимальной.
  • В случае когда требуется максимальная частота преобразователя, логично использовать полиадический преобразователь
  • В случае когда требуется минимальная латентность лучше использовать комбинационный преобразователь на базе CRT II
  • Если для задачи есть специализированный преобразователь (см. таблицу 511 512 513), то логично использовать именно его.
  • Похоже есть возможность разбить Конвеерный преобразователь на базе CRT II, на большее число этапов и тем самым повысить его эффективность. В данный момент задержка определяется последним этапом алгоритма CRT II, где сходятся максимальные модули. В итоге увеличивается общая латентность схемы и уменьшается возможная тактовая частота.

Файлы с входными данными

Файл с результатами

Источник — «https://vscripts.ru/w/index.php?title=Комплексное_исследование_обратных_преобразователей&oldid=560»