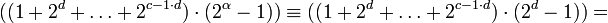Числа Мерсенна и Ферма — различия между версиями
Isaeva (обсуждение | вклад) (Новая страница: «При рассмотрении отдельных классов простых чисел значительный интерес представляет во…») |
Isaeva (обсуждение | вклад) |
||
| (не показано 13 промежуточных версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | При рассмотрении отдельных классов простых чисел значительный интерес представляет вопрос о простых числах специального вида, например, числа Мерсенна или числа Ферма. | + | При рассмотрении отдельных классов простых чисел значительный интерес представляет вопрос о простых числах специального вида, таких, например, как числа Мерсенна или числа Ферма. |
| + | |||
'''Определение''' | '''Определение''' | ||
| Строка 11: | Строка 12: | ||
При простых значениях n = p число может оказаться простым, но может быть составным. | При простых значениях n = p число может оказаться простым, но может быть составным. | ||
| − | Например, при <math>p = 2, 3, 5, 7, 13, 17, 19</math> мы получаем простые числа Мерсенна: <math>3, 7, 31, 127, 8191, 131071</math>, а при <math>p = 11, 23, 29</math> числа <math>2^p - 1</math> - составные. | + | Например, при <math>p = 2, 3, 5, 7, 13, 17, 19</math> мы получаем простые числа Мерсенна: <math>3, 7, 31, 127, 8191, 131071, 524287</math>, а при <math>p = 11, 23, 29</math> числа <math>2^p - 1</math> - составные. |
| − | + | '''Свойства чисел Мерсенна''' | |
* Если <math>M_n</math> является простым, то число ''n'' также простое. Обратное в общем случае неверно, наименьшим контрпримером является <math>M_{11} = 2047 = 23\cdot 89</math>. | * Если <math>M_n</math> является простым, то число ''n'' также простое. Обратное в общем случае неверно, наименьшим контрпримером является <math>M_{11} = 2047 = 23\cdot 89</math>. | ||
| Строка 20: | Строка 21: | ||
| − | + | Числа Мерсенна получили известность в связи с эффективным тестом простоты Люка — Лемера, благодаря которому простые числа Мерсенна давно удерживают лидерство как самые большие известные простые числа. | |
'''Определение''' | '''Определение''' | ||
| − | '''Числа Ферма''' — числа вида <math>F_n=2^{2^n}+1</math>, где ''n'' — неотрицательное целое число. | + | '''Числа Ферма''' — числа вида <math>F_n=2^{2^n}+1</math>, где ''n'' — неотрицательное целое число. |
| + | |||
При <math>n = 0, 1, 2, 3, 4</math> числа Ферма простые: <math>3, 5, 17, 257, 65537</math>. | При <math>n = 0, 1, 2, 3, 4</math> числа Ферма простые: <math>3, 5, 17, 257, 65537</math>. | ||
Все числа Мерсенна и Ферма – взаимно простые. | Все числа Мерсенна и Ферма – взаимно простые. | ||
| + | |||
| + | |||
| + | Необходимо отметить, что значения чисел Мерсенна и Ферма быстро растут. Это не позволяет ограничиться только такими числами в качестве модулей СОК. | ||
| + | |||
| + | |||
| + | '''Операции над числами Мерсенна и Ферма''' | ||
| + | |||
| + | 1. Если в качестве модулей <math>p_j</math> выбраны числа Мерсенна, т.е. числа вида <math>p_j = 2^{e_j} - 1</math>, для которых значение модуля на единицу меньше очередной степени двойки, это зачастую упрощает выполнение основных арифметических операций, так как выполнять вычисления с числами в таком представлении несколько проще, чем с числами, представленными в обратном коде. | ||
| + | |||
| + | При таком выборе модулей полезно несколько ослабить условие <math>0 \le {\alpha} < p_i</math> и потребовать только чтобы | ||
| + | |||
| + | :<math>0 \le {\alpha}_j < 2^{e_j}, a_j \equiv A \pmod{{e_j}-1} </math>. (1) | ||
| + | |||
| + | Таким образом, значение <math>{\alpha}_j = p_j = 2^{e_j}-1</math> принимается в качестве оптимального вместо <math>{\alpha}_j = 0</math>, поскольку это, с одной стороны, не влияет на справедливость китайской теоремы об остатках, а с другой означает, что math>{\alpha}_j</math> может быть любым math>{\alpha}_j</math>- битовым двоичным числом. При таком допущении, операции сложения и вычитания по модулю <math>p_j</math> выполняются следующим образом: | ||
| + | |||
| + | |||
| + | :<math>{\alpha}_j \oplus {\beta}_j = (({\alpha}_j + {\beta}_j) \pmod{e_j}) + \lfloor ({\alpha}_j + {\beta}_j) \ge 2^{e_j} \rfloor</math>, | ||
| + | |||
| + | :<math>{\alpha}_j \otimes {\beta}_j = ({\alpha}_j \cdot {\beta}_j \pmod{e_j}) \oplus \lfloor ({\alpha}_j \cdot {\beta}_j) / 2^{e_j} \rfloor</math>. | ||
| + | |||
| + | Здесь <math> \oplus </math> и <math> \otimes </math> указывают на действия, которые с учётом условия (1) должны быть выполнены с отдельными компонентами кортежей | ||
| + | <math>{\alpha}_1, {\alpha}_2, \cdots, {\alpha}_n</math> и <math>{\beta}_1, {\beta}_2, \cdots, {\beta}_n</math> при сложении или умножении соответственно. При вычитании можно пользоваться и соотношением: | ||
| + | |||
| + | :<math>{\alpha}_j \ominus {\beta}_j = (({\alpha}_j - {\beta}_j) \pmod{e_j}) - \left[ {\alpha}_j < {\beta}_j \right]</math>. | ||
| + | |||
| + | Эти операции могут быть эффективно выполнены, даже если <math>2^{e_j}</math> больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида <math>2^{e_j}-1</math> необходимо знать, при каких условиях число <math>2^{e_j}-1</math> является взаимно простым с числом <math>2^{\beta}-1</math>. Для этого существует простое правило: | ||
| + | |||
| + | :<math>(2^e-1,2^{\beta}-1) = 2^{e,\beta}-1</math>. (2) | ||
| + | |||
| + | Формула (2) утверждает, в частности, что | ||
| + | |||
| + | :<math>(2^e-1,2^{\beta}-1) = 1 \Leftrightarrow (e,\beta) = 1</math>. | ||
| + | |||
| + | Уравнение (2) следует из алгоритма Евклида и тождества | ||
| + | |||
| + | :<math>{(2^e-1)} \pmod {2^{\beta}-1} = 2^{e \pmod {b}} - 1</math>. | ||
| + | |||
| + | Поэтому на компьютере с длиной слова <math>2^{32}</math> можно выбрать | ||
| + | |||
| + | <math>p_1 = 2^{32} - 1, p_2 = 2^{31} - 1, p_3 = 2^{29} - 1, p_4 = 2^{27} - 1, p_5 = 2^{25} - 1</math>, | ||
| + | |||
| + | что обеспечивает эффективность сложения, вычитания и умножения целых чисел в интервале вплоть до <math>p_1 \cdot p_2 \cdot p_3 \cdot p_4 \cdot p_5 > 2^{143}</math>. | ||
| + | |||
| + | 2. Прямое преобразование для чисел Мерсенна | ||
| + | |||
| + | Модулярное представление <math>({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n)</math> для заданного числа <math>A</math> может быть получено посредством деления <math>A</math> на <math>(p_1, p_2, \ldots, p_n)</math> с запоминанием остатков. В случае, когда <math>A = {({\nu}_k, {\nu}_{k-1}, \ldots, {\nu}_0)}_b</math>, возможно применение более подходящего способа, который состоит в том, чтобы, используя СОК, вычислить полином | ||
| + | |||
| + | :<math>(\ldots ({\nu}_k \cdot b + {\nu}_{k-1}) \cdot b + \ldots ) b + {\nu}_0)</math>. | ||
| + | |||
| + | Если основание <math>b = 2</math> и модули <math>p_j</math> имеют вид <math>2^{e_j}-1</math>, оба подхода сводятся к совсем простому способу. | ||
| + | |||
| + | Рассмотрим двоичные представления числа <math>A</math> с блоками по <math>{e_j}</math> бит: | ||
| + | |||
| + | :<math>A = a_t \cdot N^t + a_{t-1} \cdot N^{t-1} + \ldots + a_1 \cdot N + a_0</math>, | ||
| + | |||
| + | где <math>N = 2^{e_j}</math> и <math>0 \le a_j < 2^{e_j}</math> при <math>0 \le k \le t </math>. | ||
| + | |||
| + | Тогда <math>A \equiv {(a_t + a_{t-1} + \ldots + a_1 + a_0)} \pmod {2^{e_j}-1}</math>, поскольку <math>N \equiv 1 \pmod{2^{e_j}-1}</math>. | ||
| + | |||
| + | Поэтому <math>{\alpha}_j</math> вычисляются путём сложения <math>e_j</math>-битовых чисел <math>{a_t \oplus a_{t-1} \oplus \ldots \oplus a_1 \oplus a_0} \pmod{2^{e_j}-1}</math>. | ||
| + | |||
| + | 3. Обратное преобразование для чисел Мерсенна. Алгоритм Гарнера. | ||
| + | |||
| + | Обратный переход от СОК к позиционной системе счисления несколько сложнее. Алгоритм, основанный на китайской теореме об остатках требует вычисления значение функции Эйлера для вычислении обратных мультипликативных элементов, что в общем случае требует факторизации, т.е. разложения чисел <math>p_j</math> на простые множители. Даже это показывает, что обратное преобразование чисел из СОК в позиционную систему счисления в соответствии с этим алгоритмом требует большого числа вычислительных операций с высокой точностью. | ||
| + | Алгоритм перехода от <math>{\alpha}_1, {\alpha}_2, \cdots, {\alpha}_n</math> к <math>A</math>, пригодный для практического применения, основан на доказательстве китайской теоремы об остатках, предложенном в 1958 г. Х. Л. Гарнером. Оно основано на использовании <math>{C}_n^k</math> констант <math>c_{ij} (1 \le i \le j \le k)</math>, где | ||
| + | |||
| + | :<math>c_{ij} \equiv 1 \pmod{p_j}</math>, (3) | ||
| + | |||
| + | , т.е. | ||
| + | |||
| + | :<math>c_{ij} = p_i^{-1} \pmod{p_j}</math>. | ||
| + | |||
| + | |||
| + | '''Алгоритм Гарнера''' | ||
| + | |||
| + | Рассмотрим набор модулей <math>(p_1, p_2, \dots, p_n)</math>, удовлетворяющих условию китайской теоремы об остатках. Любое число <math>0 \leqslant x < M = a_1\cdot a_2 \cdot\ldots\cdot a_n</math> однозначно представимо в виде | ||
| + | |||
| + | <math>x = x_1 + x_2\cdot p_1 + x_3\cdot p_1\cdot p_2 + \dots + x_n\cdot p_1\cdot p_2\cdot\ldots\cdot p_{n-1}</math>. | ||
| + | |||
| + | Вычислив по порядку все коэффициенты <math>x_i</math> для <math>i \in \{1, 2, \dots, n\}</math>, можно подставить их в формулу и найти искомое решение: | ||
| + | |||
| + | Рассмотрим выражение для <math>x</math> по модулю <math>p_i</math>, где <math>i\in \{2, \dots, n\}</math>, получим: | ||
| + | |||
| + | <math>x_1 = r_1</math>; | ||
| + | |||
| + | <math>r_2 = (x_1 + x_2\cdot p_1) \pmod{p_2}</math>; | ||
| + | |||
| + | <math>x_2 = (r_2 - x_1)\cdot c_{12} \pmod{p_2}</math>; | ||
| + | |||
| + | <math>r_3 = (x_1 + x_2\cdot p_1 + x_3\cdot p_1\cdot p_2) \pmod{p_3}</math>; | ||
| + | |||
| + | <math>x_3 = ((r_3 - x_1)\cdot c_{13} - x_2)\cdot c_{23} \pmod{p_3}</math> | ||
| + | |||
| + | и так далее. | ||
| + | |||
| + | Основное преимущество алгоритма Гарнера заключается в том, что вычисления производятся с числами, не превышающими величину модуля M. | ||
| + | |||
| + | Константы <math>c_{ij}</math> можно вычислить заранее с помощью расширенного алгоритма Евклида, который по заданным <math>i</math> и <math>j</math> позволяет определить числа <math>a</math> и <math>b</math> такие, что <math>a\cdot p_i + b\cdot p_j = (p_i, p_j) = 1</math>, и можно положить <math>c_{ij} = a</math>. В частности, для величины, обратной к <math>2^{\alpha} - 1</math> по модулю <math>2^{\beta} - 1</math>, легко получить сравнительно простую формулу | ||
| + | |||
| + | :<math>((1+2^d+\ldots +2^{{c-1}\cdot d})\cdot ({2^{\alpha} - 1})) \pmod {(2^{\beta} - 1)} = 1</math>, | ||
| + | |||
| + | где <math>\alpha \pmod {\beta} = d</math> и <math>c \alpha \pmod {\beta} = 1</math>. | ||
| + | |||
| + | Действительно, если <math>\alpha = {\beta} +k\cdot q</math>, то | ||
| + | |||
| + | :<math>2^{\alpha} = 2^{\beta} \cdot (2^q)^k \equiv 2^{\beta} \cdot 1^k \pmod{2^q - 1}</math>. | ||
| + | |||
| + | Поэтому при <math>2^{\alpha} \equiv 2^{\beta} \pmod{2^q - 1}</math> имеем <math>2^{{\alpha}\pmod{q}} \equiv 2^{{\beta}\pmod{q}} \pmod{2^q - 1}</math>; а так как эти последние величины расположены между нулём и <math>{2^q - 1}</math>, должно выполняться <math>{\alpha}\pmod{q} = {\beta}\pmod{q}</math>. | ||
| + | |||
| + | Тогда | ||
| + | |||
| + | :<math>((1+2^d+\ldots +2^{{c-1}\cdot d})\cdot ({2^{\alpha} - 1})) \equiv ((1+2^d+\ldots +2^{{c-1}\cdot d})\cdot (2^{d}-1)) = </math> | ||
| + | |||
| + | :<math>= 2^{cd} - 1 \equiv 2^{c\alpha} - 1 \equiv 2^1 - 1 \equiv 1\pmod {(2^{\beta} - 1)}</math>. | ||
Текущая версия на 17:43, 19 января 2015
При рассмотрении отдельных классов простых чисел значительный интерес представляет вопрос о простых числах специального вида, таких, например, как числа Мерсенна или числа Ферма.
Определение
Числа Мерсенна — числа вида 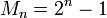 , где
, где  — натуральное число.
Названы в честь французского математика Марена Мерсенна.
— натуральное число.
Названы в честь французского математика Марена Мерсенна.
Иногда числами Мерсенна называют только числа 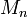 с нечетными или простыми индексами n.
с нечетными или простыми индексами n.
Множества простых чисел в этих последовательностях совпадают, а потому понятие простого числа Мерсенна не зависит от того, как именно определяются числа Мерсенна.
При простых значениях n = p число может оказаться простым, но может быть составным.
Например, при 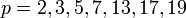 мы получаем простые числа Мерсенна:
мы получаем простые числа Мерсенна:  , а при
, а при 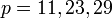 числа
числа 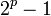 - составные.
- составные.
Свойства чисел Мерсенна
- Если
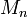 является простым, то число n также простое. Обратное в общем случае неверно, наименьшим контрпримером является
является простым, то число n также простое. Обратное в общем случае неверно, наименьшим контрпримером является 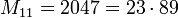 .
.
- Любой делитель числа
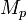 для простого p имеет вид 2pk+1, где k — натуральное число (следствие малой теоремы Ферма).
для простого p имеет вид 2pk+1, где k — натуральное число (следствие малой теоремы Ферма).
Числа Мерсенна получили известность в связи с эффективным тестом простоты Люка — Лемера, благодаря которому простые числа Мерсенна давно удерживают лидерство как самые большие известные простые числа.
Определение
Числа Ферма — числа вида 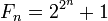 , где n — неотрицательное целое число.
, где n — неотрицательное целое число.
При 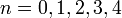 числа Ферма простые:
числа Ферма простые: 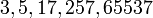 .
.
Все числа Мерсенна и Ферма – взаимно простые.
Необходимо отметить, что значения чисел Мерсенна и Ферма быстро растут. Это не позволяет ограничиться только такими числами в качестве модулей СОК.
Операции над числами Мерсенна и Ферма
1. Если в качестве модулей 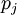 выбраны числа Мерсенна, т.е. числа вида
выбраны числа Мерсенна, т.е. числа вида 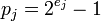 , для которых значение модуля на единицу меньше очередной степени двойки, это зачастую упрощает выполнение основных арифметических операций, так как выполнять вычисления с числами в таком представлении несколько проще, чем с числами, представленными в обратном коде.
, для которых значение модуля на единицу меньше очередной степени двойки, это зачастую упрощает выполнение основных арифметических операций, так как выполнять вычисления с числами в таком представлении несколько проще, чем с числами, представленными в обратном коде.
При таком выборе модулей полезно несколько ослабить условие 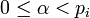 и потребовать только чтобы
и потребовать только чтобы
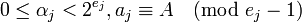 . (1)
. (1)
Таким образом, значение 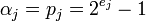 принимается в качестве оптимального вместо
принимается в качестве оптимального вместо 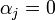 , поскольку это, с одной стороны, не влияет на справедливость китайской теоремы об остатках, а с другой означает, что math>{\alpha}_j</math> может быть любым math>{\alpha}_j</math>- битовым двоичным числом. При таком допущении, операции сложения и вычитания по модулю
, поскольку это, с одной стороны, не влияет на справедливость китайской теоремы об остатках, а с другой означает, что math>{\alpha}_j</math> может быть любым math>{\alpha}_j</math>- битовым двоичным числом. При таком допущении, операции сложения и вычитания по модулю 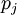 выполняются следующим образом:
выполняются следующим образом:
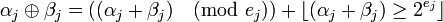 ,
,
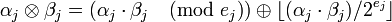 .
.
Здесь 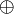 и
и 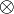 указывают на действия, которые с учётом условия (1) должны быть выполнены с отдельными компонентами кортежей
указывают на действия, которые с учётом условия (1) должны быть выполнены с отдельными компонентами кортежей
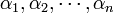 и
и 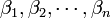 при сложении или умножении соответственно. При вычитании можно пользоваться и соотношением:
при сложении или умножении соответственно. При вычитании можно пользоваться и соотношением:
![{\alpha}_j \ominus {\beta}_j = (({\alpha}_j - {\beta}_j) \pmod{e_j}) - \left[ {\alpha}_j < {\beta}_j \right]](/w/images/math/7/6/3/76346ef84c71fa3f5fd9b95984b7594f.png) .
.
Эти операции могут быть эффективно выполнены, даже если 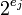 больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида
больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида 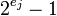 необходимо знать, при каких условиях число
необходимо знать, при каких условиях число 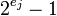 является взаимно простым с числом
является взаимно простым с числом 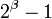 . Для этого существует простое правило:
. Для этого существует простое правило:
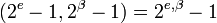 . (2)
. (2)
Формула (2) утверждает, в частности, что
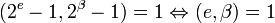 .
.
Уравнение (2) следует из алгоритма Евклида и тождества
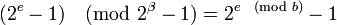 .
.
Поэтому на компьютере с длиной слова 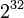 можно выбрать
можно выбрать
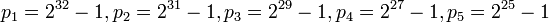 ,
,
что обеспечивает эффективность сложения, вычитания и умножения целых чисел в интервале вплоть до 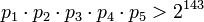 .
.
2. Прямое преобразование для чисел Мерсенна
Модулярное представление 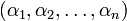 для заданного числа
для заданного числа  может быть получено посредством деления
может быть получено посредством деления  на
на 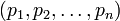 с запоминанием остатков. В случае, когда
с запоминанием остатков. В случае, когда 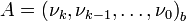 , возможно применение более подходящего способа, который состоит в том, чтобы, используя СОК, вычислить полином
, возможно применение более подходящего способа, который состоит в том, чтобы, используя СОК, вычислить полином
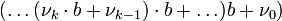 .
.
Если основание 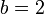 и модули
и модули 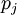 имеют вид
имеют вид 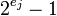 , оба подхода сводятся к совсем простому способу.
, оба подхода сводятся к совсем простому способу.
Рассмотрим двоичные представления числа  с блоками по
с блоками по 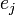 бит:
бит:
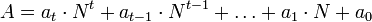 ,
,
где 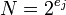 и
и 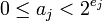 при
при 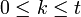 .
.
Тогда 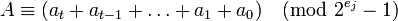 , поскольку
, поскольку 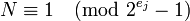 .
.
Поэтому 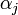 вычисляются путём сложения
вычисляются путём сложения 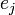 -битовых чисел
-битовых чисел 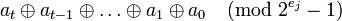 .
.
3. Обратное преобразование для чисел Мерсенна. Алгоритм Гарнера.
Обратный переход от СОК к позиционной системе счисления несколько сложнее. Алгоритм, основанный на китайской теореме об остатках требует вычисления значение функции Эйлера для вычислении обратных мультипликативных элементов, что в общем случае требует факторизации, т.е. разложения чисел 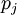 на простые множители. Даже это показывает, что обратное преобразование чисел из СОК в позиционную систему счисления в соответствии с этим алгоритмом требует большого числа вычислительных операций с высокой точностью.
Алгоритм перехода от
на простые множители. Даже это показывает, что обратное преобразование чисел из СОК в позиционную систему счисления в соответствии с этим алгоритмом требует большого числа вычислительных операций с высокой точностью.
Алгоритм перехода от 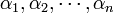 к
к  , пригодный для практического применения, основан на доказательстве китайской теоремы об остатках, предложенном в 1958 г. Х. Л. Гарнером. Оно основано на использовании
, пригодный для практического применения, основан на доказательстве китайской теоремы об остатках, предложенном в 1958 г. Х. Л. Гарнером. Оно основано на использовании 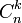 констант
констант 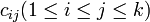 , где
, где
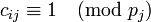 , (3)
, (3)
, т.е.
 .
.
Алгоритм Гарнера
Рассмотрим набор модулей 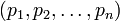 , удовлетворяющих условию китайской теоремы об остатках. Любое число
, удовлетворяющих условию китайской теоремы об остатках. Любое число 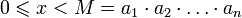 однозначно представимо в виде
однозначно представимо в виде
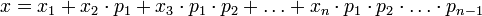 .
.
Вычислив по порядку все коэффициенты 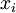 для
для 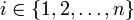 , можно подставить их в формулу и найти искомое решение:
, можно подставить их в формулу и найти искомое решение:
Рассмотрим выражение для  по модулю
по модулю 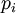 , где
, где 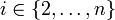 , получим:
, получим:
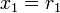 ;
;
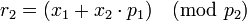 ;
;
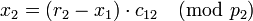 ;
;
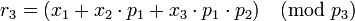 ;
;
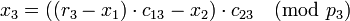
и так далее.
Основное преимущество алгоритма Гарнера заключается в том, что вычисления производятся с числами, не превышающими величину модуля M.
Константы 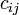 можно вычислить заранее с помощью расширенного алгоритма Евклида, который по заданным
можно вычислить заранее с помощью расширенного алгоритма Евклида, который по заданным 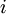 и
и 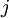 позволяет определить числа
позволяет определить числа  и
и  такие, что
такие, что 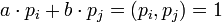 , и можно положить
, и можно положить 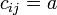 . В частности, для величины, обратной к
. В частности, для величины, обратной к 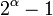 по модулю
по модулю 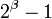 , легко получить сравнительно простую формулу
, легко получить сравнительно простую формулу
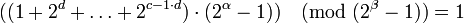 ,
,
где 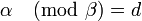 и
и 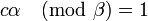 .
.
Действительно, если 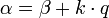 , то
, то
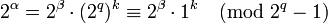 .
.
Поэтому при 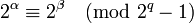 имеем
имеем  ; а так как эти последние величины расположены между нулём и
; а так как эти последние величины расположены между нулём и 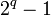 , должно выполняться
, должно выполняться 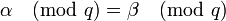 .
.
Тогда
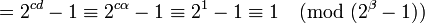 .
.