Числа Мерсенна и Ферма — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 56: | Строка 56: | ||
:<math>{\alpha}_j \ominus {\beta}_j = ({\alpha}_j - {\beta}_j \pmod{e_j}) - \left[ {\alpha}_j < {\beta}_j \right]</math>. | :<math>{\alpha}_j \ominus {\beta}_j = ({\alpha}_j - {\beta}_j \pmod{e_j}) - \left[ {\alpha}_j < {\beta}_j \right]</math>. | ||
| + | |||
| + | Эти операции могут быть эффективно выполнены, даже если <math>2^{e_j}</math> больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида <math>2^{e_j}-1</math> необходимо знать, при каких условиях число <math>2^{e_j}-1</math> является взаимно простым с числом <math>2^{\beta}-1</math>. Для этого существует простое правило: | ||
| + | |||
| + | :<math>(2^e-1,2^{\beta}-1) = 2^{e,\beta}-1</math>. (2) | ||
| + | |||
| + | Формула (2) утверждает, в частности, что | ||
| + | |||
| + | :<math>(2^e-1,2^{\beta}-1) = 1 \Leftrightarrow (e,\beta) = 1</math>. | ||
| + | |||
| + | Уравнение (2) следует из алгоритма Евклида и тождества | ||
| + | |||
| + | :<math>{(2^e-1)} \pmod {2^{\beta}-1} = 2^{e \pmod {b}} - 1</math>. | ||
| + | |||
| + | Поэтому на компьютере с длиной слова <math>2^{32}</math> можно выбрать | ||
| + | |||
| + | <math>p_1 = 2^{32} - 1, p_2 = 2^{31} - 1, p_3 = 2^{29} - 1, p_4 = 2^{27} - 1, p_5 = 2^{25} - 1</math>, | ||
| + | |||
| + | что обеспечивает эффективность сложения, вычитания и умножения целых чисел в интервале вплоть до <math>p_1 \cdot p_2 \cdot p_3 \cdot p_4 \cdot p_5 > 2^{143}</math>. | ||
Версия 15:40, 25 декабря 2014
При рассмотрении отдельных классов простых чисел значительный интерес представляет вопрос о простых числах специального вида, например, числа Мерсенна или числа Ферма.
Определение
Числа Мерсенна — числа вида 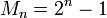 , где
, где  — натуральное число.
Названы в честь французского математика Марена Мерсенна.
— натуральное число.
Названы в честь французского математика Марена Мерсенна.
Иногда числами Мерсенна называют только числа 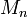 с нечетными или простыми индексами n.
с нечетными или простыми индексами n.
Множества простых чисел в этих последовательностях совпадают, а потому понятие простого числа Мерсенна не зависит от того, как именно определяются числа Мерсенна.
При простых значениях n = p число может оказаться простым, но может быть составным.
Например, при 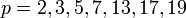 мы получаем простые числа Мерсенна:
мы получаем простые числа Мерсенна: 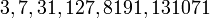 , а при
, а при 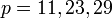 числа
числа 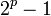 - составные.
- составные.
Свойства чисел Мерсенна
- Если
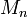 является простым, то число n также простое. Обратное в общем случае неверно, наименьшим контрпримером является
является простым, то число n также простое. Обратное в общем случае неверно, наименьшим контрпримером является 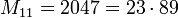 .
.
- Любой делитель числа
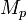 для простого p имеет вид 2pk+1, где k — натуральное число (следствие малой теоремы Ферма).
для простого p имеет вид 2pk+1, где k — натуральное число (следствие малой теоремы Ферма).
Числа Мерсенна получили известность в связи с эффективным тестом простоты Люка — Лемера, благодаря которому простые числа Мерсенна давно удерживают лидерство как самые большие известные простые числа.
Определение
Числа Ферма — числа вида 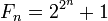 , где n — неотрицательное целое число.
, где n — неотрицательное целое число.
При 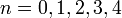 числа Ферма простые:
числа Ферма простые: 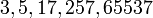 .
.
Все числа Мерсенна и Ферма – взаимно простые.
Необходимо отметить, что значения чисел Мерсенна и Ферма быстро растут. Это не позволяет только такими числами в качестве модулей СОК.
Операции над числами Мерсенна и Ферма
1. Если в качестве модулей 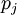 выбраны числа Мерсенна, т.е. числа вида
выбраны числа Мерсенна, т.е. числа вида 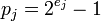 , для которых значение модуля на единицу меньше очередной степени двойки, это зачастую упрощает выполнение основных арифметических операций, так как выполнять вычисления с числами в таком представлении несколько проще, чем с числами, представленными в обратном коде.
, для которых значение модуля на единицу меньше очередной степени двойки, это зачастую упрощает выполнение основных арифметических операций, так как выполнять вычисления с числами в таком представлении несколько проще, чем с числами, представленными в обратном коде.
При таком выборе модулей полезно несколько ослабить условие 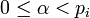 и потребовать только чтобы
и потребовать только чтобы
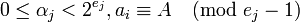 . (1)
. (1)
Таким образом, значение 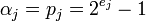 принимается в качестве оптимального вместо
принимается в качестве оптимального вместо 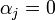 , поскольку это, с одной стороны, не влияет на справедливость китайской теоремы об остатках, а с другой означает, что math>{\alpha}_j</math> может быть любым math>{\alpha}_j</math>- битовым двоичным числом. При таком допущении, операции сложения и вычитания по модулю
, поскольку это, с одной стороны, не влияет на справедливость китайской теоремы об остатках, а с другой означает, что math>{\alpha}_j</math> может быть любым math>{\alpha}_j</math>- битовым двоичным числом. При таком допущении, операции сложения и вычитания по модулю 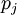 выполняются следующим образом:
выполняются следующим образом:
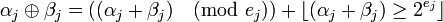 ,
,
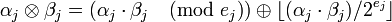 .
.
Здесь 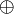 и
и 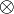 указывают на действия, которые с учётом условия (1) должны быть выполнены с отдельными компонентами кортежей
указывают на действия, которые с учётом условия (1) должны быть выполнены с отдельными компонентами кортежей
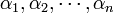 и
и 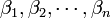 при сложении или умножении соответственно. При вычитании можно пользоваться и соотношением:
при сложении или умножении соответственно. При вычитании можно пользоваться и соотношением:
![{\alpha}_j \ominus {\beta}_j = ({\alpha}_j - {\beta}_j \pmod{e_j}) - \left[ {\alpha}_j < {\beta}_j \right]](/w/images/math/2/2/d/22d309647472d9073de963781fc82965.png) .
.
Эти операции могут быть эффективно выполнены, даже если 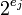 больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида
больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида 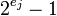 необходимо знать, при каких условиях число
необходимо знать, при каких условиях число 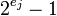 является взаимно простым с числом
является взаимно простым с числом 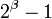 . Для этого существует простое правило:
. Для этого существует простое правило:
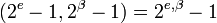 . (2)
. (2)
Формула (2) утверждает, в частности, что
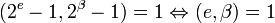 .
.
Уравнение (2) следует из алгоритма Евклида и тождества
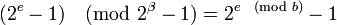 .
.
Поэтому на компьютере с длиной слова 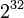 можно выбрать
можно выбрать
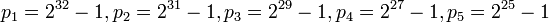 ,
,
что обеспечивает эффективность сложения, вычитания и умножения целых чисел в интервале вплоть до 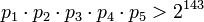 .
.