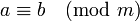Сравнения и их основные свойства — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 45: | Строка 45: | ||
Другие свойства: | Другие свойства: | ||
| − | * Если <math>a \equiv b \pmod m</math> и k – произвольное целое число, то <math> k \cdot a \equiv k \cdot b \pmod m</math>. | + | * Если <math>a \equiv b \pmod m</math> и <math>k</math> – произвольное целое число, то <math> k \cdot a \equiv k \cdot b \pmod m</math>. |
* Если <math> k \cdot a \equiv k \cdot b \pmod m </math> и <math> (k, m) = 1 </math>, то <math>a \equiv b \pmod m</math>. | * Если <math> k \cdot a \equiv k \cdot b \pmod m </math> и <math> (k, m) = 1 </math>, то <math>a \equiv b \pmod m</math>. | ||
| − | * Если <math>a \equiv b \pmod m | + | * Если <math>a \equiv b \pmod m</math> и k – произвольное натуральное число, то <math> k \cdot a \equiv k \cdot b \pmod {k \cdot m}</math>. |
| − | * Если <math> k \cdot a \equiv k \cdot b \pmod {k \cdot m}</math>, где k и m – произвольные натуральные числа, то <math>a \equiv b \pmod m</math>. | + | * Если <math> k \cdot a \equiv k \cdot b \pmod {k \cdot m}</math>, где <math>k</math> и <math>m</math> – произвольные натуральные числа, то <math>a \equiv b \pmod m</math>. |
| + | |||
| + | * Если <math>a \equiv b \pmod m</math> и <math>c \equiv d \pmod m</math>, то <math>a+c \equiv b+d \pmod m</math> и <math>a-c \equiv b-d \pmod m</math>. | ||
| + | |||
| + | * Если <math>a \equiv b \pmod m</math> и <math>c \equiv d \pmod m</math>, то <math>a \cdot c \equiv b \cdot d \pmod m</math>. | ||
| + | |||
| + | * Если <math>a \equiv b \pmod m</math> и <math>f(x) = c_0 + c_1 \cdot x_1 + \ldots + c_n \cdot x_n</math> - произвольный многочлен с целыми коэффициентами, то <math>f(a) = f(b) \pmod m</math>. | ||
| + | |||
| + | * Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть. | ||
| + | |||
| + | * Если <math>a \equiv b \pmod m</math> и <math>d/m</math>, то <math>a \equiv b \pmod d</math>. | ||
| + | |||
| + | * Если <math>a \equiv b \pmod m</math>, то множество общих делителей <math>a</math> и <math>m</math> совпадает с множеством общих делителей <math>b</math> и <math>m</math>. В частности, <math>(a,m) = (b,m)</math>. | ||
| + | |||
| + | * Если <math>a \equiv b \pmod m_1, a \equiv b \pmod m_2, \ldots, a \equiv b \pmod m_s</math>, то <math>a \equiv b \pmod m</math>, где <math>m = [m_1, m_2, \ldots, m_s]</math>. | ||
Версия 09:44, 23 января 2015
Возьмём произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на
и будем рассматривать остатки при делении на  различных целых чисел.
различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Содержание
Определения
Определение. Два целых числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если их разность
, если их разность 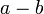 делится без остатка на
делится без остатка на  .
.
Символически сравнимость записывается в виде формулы (сравнения):
Число  называется модулем сравнения.
называется модулем сравнения.
Если разность 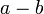 не делится на
не делится на  , то запишем:
, то запишем:
-
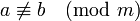 .
.
Согласно определению, 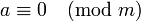 означает, что
означает, что  делится на
делится на  .
.
Теорема.  сравнимо с
сравнимо с  тогда и только тогда, когда
тогда и только тогда, когда  и
и  имеют одинаковые остатки при делении на
имеют одинаковые остатки при делении на  .
Поэтому в качестве определения сравнения можно взять следующую эквивалентную формулировку:
.
Поэтому в качестве определения сравнения можно взять следующую эквивалентную формулировку:
Определение. Целые числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если остатки от деления этих чисел на
, если остатки от деления этих чисел на  равны.
равны.
Примеры
-
 , т. к. 101 – 17 = 84, а 84 делится без остатка на 21.
, т. к. 101 – 17 = 84, а 84 делится без остатка на 21.
-
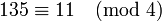 , т. к. оба числа 135 и 11 при делении на 4 дают остаток 3.
, т. к. оба числа 135 и 11 при делении на 4 дают остаток 3.
Свойства
Для фиксированного натурального числа  отношение сравнимости по модулю
отношение сравнимости по модулю  обладает следующими свойствами:
обладает следующими свойствами:
- Рефлексивность: для любого целого
 справедливо
справедливо 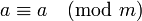 .
.
- Симметричность: если
 , то
, то 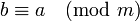 .
.
- Транзитивность: если
 и
и 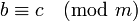 , то
, то 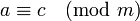 .
.
Таким образом, отношение сравнимости по модулю  является отношением эквивалентности на множестве целых чисел.
является отношением эквивалентности на множестве целых чисел.
Другие свойства:
- Если
 и
и 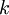 – произвольное целое число, то
– произвольное целое число, то 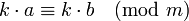 .
.
- Если
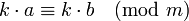 и
и 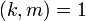 , то
, то  .
.
- Если
 и k – произвольное натуральное число, то
и k – произвольное натуральное число, то  .
.
- Если
 , где
, где 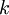 и
и  – произвольные натуральные числа, то
– произвольные натуральные числа, то  .
.
- Если
 и
и 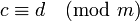 , то
, то 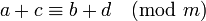 и
и 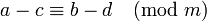 .
.
- Если
 и
и 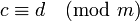 , то
, то 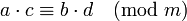 .
.
- Если
 и
и 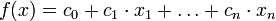 - произвольный многочлен с целыми коэффициентами, то
- произвольный многочлен с целыми коэффициентами, то 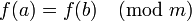 .
.
- Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть.
- Если
 и
и 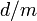 , то
, то 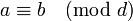 .
.
- Если
 , то множество общих делителей
, то множество общих делителей  и
и  совпадает с множеством общих делителей
совпадает с множеством общих делителей  и
и  . В частности,
. В частности, 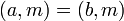 .
.
- Если
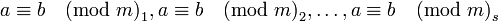 , то
, то  , где
, где ![m = [m_1, m_2, \ldots, m_s]](/w/images/math/9/1/c/91cfa423b902ea14a3811c08c0bd6d0d.png) .
.
Классы вычетов
Отнесём все целые числа, дающие при делении на  один и тот же остаток в один класс, поэтому получится
один и тот же остаток в один класс, поэтому получится  различных классов по модулю
различных классов по модулю  .
.
Множество всех чисел сравнимых с  по модулю
по модулю  называется классом вычетов
называется классом вычетов  по модулю
по модулю  .
.