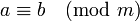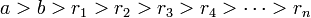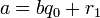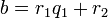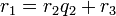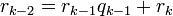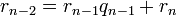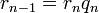Система остаточных классов - введение — различия между версиями
Turbo (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 20: | Строка 20: | ||
| − | Определение. Два целых числа <math> a </math>и <math> b </math>называются '''сравнимыми по модулю m''', если их разность <math> a | + | Определение. Два целых числа <math> a </math> и <math> b </math> называются '''сравнимыми по модулю <math> m </math>''', если их разность <math> a-b </math> делится без остатка на <math> m </math>. |
Символически сравнимость записывается в виде формулы ('''сравнения'''): | Символически сравнимость записывается в виде формулы ('''сравнения'''): | ||
| Строка 29: | Строка 29: | ||
Эквивалентная формулировка: | Эквивалентная формулировка: | ||
| − | Определение. Целые числа <math> a </math>и <math> b </math>называются '''сравнимыми по модулю m''', если остатки от деления этих чисел на<math> m </math> равны. | + | Определение. Целые числа <math> a </math> и <math> b </math> называются '''сравнимыми по модулю <math> m </math>''', если остатки от деления этих чисел на <math> m </math> равны. |
Отношение сравнимости по модулю <math> m </math> обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности. | Отношение сравнимости по модулю <math> m </math> обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности. | ||
Версия 09:44, 28 августа 2014
Содержание
Теоретико-числовая база построения системы остаточных классов
Напомним определение деления с остатком.
Определение. Говорят, что целое число 
делится на натуральное число 
с остатком, если имеется пара целых чисел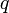 
и 
, таких, что 
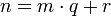и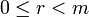 
.
называется делимым, - делителем, 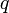- неполным частным, - остатком.
Для целых чисел:
Определение. Говорят, что целое число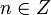 
делится на натуральное число 
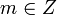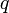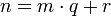с остатком, если имеется пара целых чисел и , таких, что и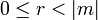 
.
Пример: 48 при делении на 5 даёт остаток 3, т.к.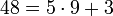 
, 
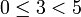, -48 при делении на 5 даёт остаток 2, т.к. 
, 
.
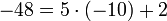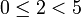Сравнения и их основные свойства
Возьмём произвольное фиксированное натуральное число и будем рассматривать остатки при делении на различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Определение. Два целых числа 
и 
называются сравнимыми по модулю , если их разность 
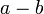делится без остатка на .
Символически сравнимость записывается в виде формулы (сравнения):
Число называется модулем сравнения.
Эквивалентная формулировка:
Определение. Целые числа и называются сравнимыми по модулю , если остатки от деления этих чисел на равны.
Отношение сравнимости по модулю обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
Отнесём все целые числа, дающие при делении на один и тот же остаток в один класс, поэтому получится различных классов по модулю .
Множество всех чисел сравнимых с по модулю называется классом вычетов по модулю .
Подробнее о свойствах сравнений и классах вычетов смотри Сравнения и их основные свойства
Теорема о делении с остатком. Алгоритм Евклида
Теорема о делении с остатком
для любых целых a и b,
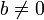, существует единственный набор целых чисел q и r, что a = bq + r и 
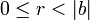, где |b| — модуль числа b.
На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.
Алгоритм Евклида для целых чисел
Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое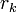 
— это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
Тогда НОД(a,b), наибольший общий делитель и , равен
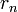, последнему ненулевому члену этой последовательности.
Существование таких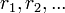 
, то есть возможность деления с остатком на для любого целого и целого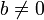 
, доказывается индукцией.
Корректность этого алгоритма вытекает из следующих двух утверждений:
- Пусть
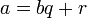, тогда НОД (, ) = НОД (, ).
- НОД(0,) = для любого ненулевого (так как 0 делится на любое целое число, кроме нуля).
