Числа Мерсенна и Ферма — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 131: | Строка 131: | ||
Константы <math>c_{ij}</math> можно вычислить заранее с помощью расширенного алгоритма Евклида, который по заданным <math>i</math> и <math>j</math> позволяет определить числа <math>a</math> и <math>b</math> такие, что <math>a\cdot p_i + b\cdot p_j = (p_i, p_j) = 1</math>, и можно положить <math>c_{ij} = a</math>. В частности, для величины, обратной к <math>2^{\alpha} - 1</math> по модулю <math>2^{\beta} - 1</math>, легко получить сравнительно простую формулу | Константы <math>c_{ij}</math> можно вычислить заранее с помощью расширенного алгоритма Евклида, который по заданным <math>i</math> и <math>j</math> позволяет определить числа <math>a</math> и <math>b</math> такие, что <math>a\cdot p_i + b\cdot p_j = (p_i, p_j) = 1</math>, и можно положить <math>c_{ij} = a</math>. В частности, для величины, обратной к <math>2^{\alpha} - 1</math> по модулю <math>2^{\beta} - 1</math>, легко получить сравнительно простую формулу | ||
| − | :<math>((1+2^d+\ldots +2^{{c-1}\cdot d})\ | + | :<math>((1+2^d+\ldots +2^{{c-1}\cdot d})\cdot ({2^{\alpha} - 1})) \pmod {(2^{\beta} - 1)} = 1</math>, |
| − | где <math>\alpha \pmod {\beta} = d</math> и <math>c\alpha \pmod {\beta} = 1</math>. | + | где <math>\alpha \pmod {\beta} = d</math> и <math>c \alpha \pmod {\beta} = 1</math>. |
Действительно, если <math>\alpha = {\beta} +k\cdot q</math>, то | Действительно, если <math>\alpha = {\beta} +k\cdot q</math>, то | ||
Версия 09:37, 19 января 2015
При рассмотрении отдельных классов простых чисел значительный интерес представляет вопрос о простых числах специального вида, таких, например, как числа Мерсенна или числа Ферма.
Определение
Числа Мерсенна — числа вида 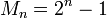 , где
, где 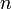 — натуральное число.
Названы в честь французского математика Марена Мерсенна.
— натуральное число.
Названы в честь французского математика Марена Мерсенна.
Иногда числами Мерсенна называют только числа 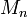 с нечетными или простыми индексами n.
с нечетными или простыми индексами n.
Множества простых чисел в этих последовательностях совпадают, а потому понятие простого числа Мерсенна не зависит от того, как именно определяются числа Мерсенна.
При простых значениях n = p число может оказаться простым, но может быть составным.
Например, при 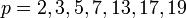 мы получаем простые числа Мерсенна:
мы получаем простые числа Мерсенна: 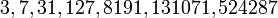 , а при
, а при 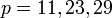 числа
числа 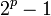 - составные.
- составные.
Свойства чисел Мерсенна
- Если
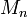 является простым, то число n также простое. Обратное в общем случае неверно, наименьшим контрпримером является
является простым, то число n также простое. Обратное в общем случае неверно, наименьшим контрпримером является 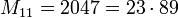 .
.
- Любой делитель числа
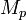 для простого p имеет вид 2pk+1, где k — натуральное число (следствие малой теоремы Ферма).
для простого p имеет вид 2pk+1, где k — натуральное число (следствие малой теоремы Ферма).
Числа Мерсенна получили известность в связи с эффективным тестом простоты Люка — Лемера, благодаря которому простые числа Мерсенна давно удерживают лидерство как самые большие известные простые числа.
Определение
Числа Ферма — числа вида 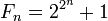 , где n — неотрицательное целое число.
, где n — неотрицательное целое число.
При 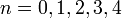 числа Ферма простые:
числа Ферма простые: 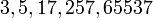 .
.
Все числа Мерсенна и Ферма – взаимно простые.
Необходимо отметить, что значения чисел Мерсенна и Ферма быстро растут. Это не позволяет ограничиться только такими числами в качестве модулей СОК.
Операции над числами Мерсенна и Ферма
1. Если в качестве модулей 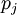 выбраны числа Мерсенна, т.е. числа вида
выбраны числа Мерсенна, т.е. числа вида 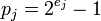 , для которых значение модуля на единицу меньше очередной степени двойки, это зачастую упрощает выполнение основных арифметических операций, так как выполнять вычисления с числами в таком представлении несколько проще, чем с числами, представленными в обратном коде.
, для которых значение модуля на единицу меньше очередной степени двойки, это зачастую упрощает выполнение основных арифметических операций, так как выполнять вычисления с числами в таком представлении несколько проще, чем с числами, представленными в обратном коде.
При таком выборе модулей полезно несколько ослабить условие 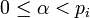 и потребовать только чтобы
и потребовать только чтобы
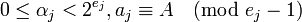 . (1)
. (1)
Таким образом, значение 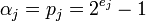 принимается в качестве оптимального вместо
принимается в качестве оптимального вместо 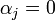 , поскольку это, с одной стороны, не влияет на справедливость китайской теоремы об остатках, а с другой означает, что math>{\alpha}_j</math> может быть любым math>{\alpha}_j</math>- битовым двоичным числом. При таком допущении, операции сложения и вычитания по модулю
, поскольку это, с одной стороны, не влияет на справедливость китайской теоремы об остатках, а с другой означает, что math>{\alpha}_j</math> может быть любым math>{\alpha}_j</math>- битовым двоичным числом. При таком допущении, операции сложения и вычитания по модулю  выполняются следующим образом:
выполняются следующим образом:
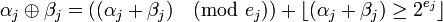 ,
,
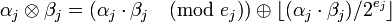 .
.
Здесь 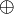 и
и 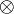 указывают на действия, которые с учётом условия (1) должны быть выполнены с отдельными компонентами кортежей
указывают на действия, которые с учётом условия (1) должны быть выполнены с отдельными компонентами кортежей
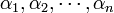 и
и 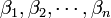 при сложении или умножении соответственно. При вычитании можно пользоваться и соотношением:
при сложении или умножении соответственно. При вычитании можно пользоваться и соотношением:
![{\alpha}_j \ominus {\beta}_j = (({\alpha}_j - {\beta}_j) \pmod{e_j}) - \left[ {\alpha}_j < {\beta}_j \right]](/w/images/math/7/6/3/76346ef84c71fa3f5fd9b95984b7594f.png) .
.
Эти операции могут быть эффективно выполнены, даже если 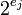 больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида
больше машинного слова компьютера, так как совсем просто вычислить остаток положительного числа по модулю степени 2 или разложить число по степеням 2. Для работы с модулями вида 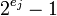 необходимо знать, при каких условиях число
необходимо знать, при каких условиях число 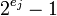 является взаимно простым с числом
является взаимно простым с числом 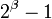 . Для этого существует простое правило:
. Для этого существует простое правило:
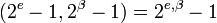 . (2)
. (2)
Формула (2) утверждает, в частности, что
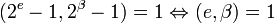 .
.
Уравнение (2) следует из алгоритма Евклида и тождества
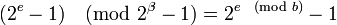 .
.
Поэтому на компьютере с длиной слова 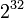 можно выбрать
можно выбрать
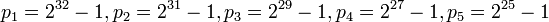 ,
,
что обеспечивает эффективность сложения, вычитания и умножения целых чисел в интервале вплоть до 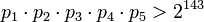 .
.
2. Прямое преобразование для чисел Мерсенна
Модулярное представление 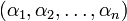 для заданного числа
для заданного числа  может быть получено посредством деления
может быть получено посредством деления 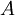 на
на 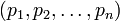 с запоминанием остатков. В случае, когда
с запоминанием остатков. В случае, когда 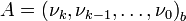 , возможно применение более подходящего способа, который состоит в том, чтобы, используя СОК, вычислить полином
, возможно применение более подходящего способа, который состоит в том, чтобы, используя СОК, вычислить полином
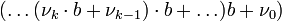 .
.
Если основание  и модули
и модули  имеют вид
имеют вид 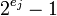 , оба подхода сводятся к совсем простому способу.
, оба подхода сводятся к совсем простому способу.
Рассмотрим двоичные представления числа  с блоками по
с блоками по  бит:
бит:
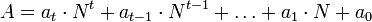 ,
,
где 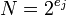 и
и 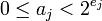 при
при 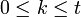 .
.
Тогда 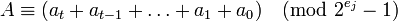 , поскольку
, поскольку 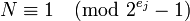 .
.
Поэтому 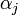 вычисляются путём сложения
вычисляются путём сложения 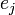 -битовых чисел
-битовых чисел 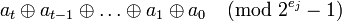 .
.
3. Обратное преобразование для чисел Мерсенна. Алгоритм Гарнера.
Обратный переход от СОК к позиционной системе счисления несколько сложнее. Алгоритм, основанный на китайской теореме об остатках требует вычисления значение функции Эйлера для вычислении обратных мультипликативных элементов, что в общем случае требует факторизации, т.е. разложения чисел 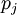 на простые множители. Даже это показывает, что обратное преобразование чисел из СОК в позиционную систему счисления в соответствии с этим алгоритмом требует большого числа вычислительных операций с высокой точностью.
Алгоритм перехода от
на простые множители. Даже это показывает, что обратное преобразование чисел из СОК в позиционную систему счисления в соответствии с этим алгоритмом требует большого числа вычислительных операций с высокой точностью.
Алгоритм перехода от 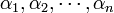 к
к  , пригодный для практического применения, основан на доказательстве китайской теоремы об остатках, предложенном в 1958 г. Х. Л. Гарнером. Оно основано на использовании
, пригодный для практического применения, основан на доказательстве китайской теоремы об остатках, предложенном в 1958 г. Х. Л. Гарнером. Оно основано на использовании 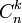 констант
констант 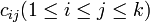 , где
, где
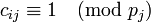 , (3)
, (3)
, т.е.
 .
.
Алгоритм Гарнера
Рассмотрим набор модулей 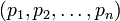 , удовлетворяющих условию китайской теоремы об остатках. Любое число
, удовлетворяющих условию китайской теоремы об остатках. Любое число 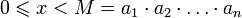 однозначно представимо в виде
однозначно представимо в виде
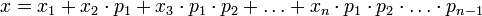 .
.
Вычислив по порядку все коэффициенты 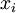 для
для 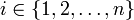 , можно подставить их в формулу и найти искомое решение:
, можно подставить их в формулу и найти искомое решение:
Рассмотрим выражение для 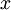 по модулю
по модулю 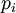 , где
, где 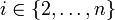 , получим:
, получим:
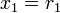 ;
;
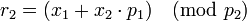 ;
;
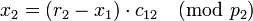 ;
;
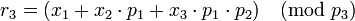 ;
;
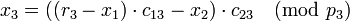
и так далее.
Основное преимущество алгоритма Гарнера заключается в том, что вычисления производятся с числами, не превышающими величину модуля M.
Константы 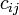 можно вычислить заранее с помощью расширенного алгоритма Евклида, который по заданным
можно вычислить заранее с помощью расширенного алгоритма Евклида, который по заданным 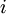 и
и 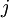 позволяет определить числа
позволяет определить числа  и
и  такие, что
такие, что 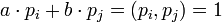 , и можно положить
, и можно положить 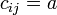 . В частности, для величины, обратной к
. В частности, для величины, обратной к 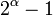 по модулю
по модулю 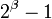 , легко получить сравнительно простую формулу
, легко получить сравнительно простую формулу
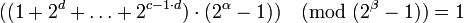 ,
,
где 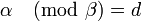 и
и 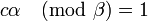 .
.
Действительно, если 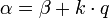 , то
, то
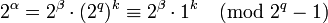 .
.
Поэтому при 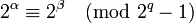 имеем
имеем  ; а так как эти последние величины расположены между нулём и
; а так как эти последние величины расположены между нулём и 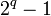 , должно выполняться
, должно выполняться 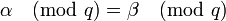 .
.
Тогда