Результаты синтеза прямых/обратных преобразователей на спец модулях вида 2^n-1, 2^n, 2^n+1 для Д.Д. до 64 бит. — различия между версиями
Материал из Модулярная арифметики
DimaT (обсуждение | вклад) (Новая страница: «Для того чтобы проанализировать конкурентоспособность модулярной арифметики, были про…») |
DimaT (обсуждение | вклад) (→Типовые Verilog-модули) |
||
| Строка 1: | Строка 1: | ||
Для того чтобы проанализировать конкурентоспособность модулярной арифметики, были проведены тесты прямых/обратных преобразователей для спец модулей вида <math>(2^n-1, 2^n, 2^n+1)</math>. Сравнение производилось для широкого динамического диапазона до 128 бит. Соответственно, параметр <math>n</math> варьировался от 3 до 43. Методы построения преобразователей были заимствованы из книги ''Residue number systems: Theory and implementation (Amos Omondi, Benjamin Premkumar)''. | Для того чтобы проанализировать конкурентоспособность модулярной арифметики, были проведены тесты прямых/обратных преобразователей для спец модулей вида <math>(2^n-1, 2^n, 2^n+1)</math>. Сравнение производилось для широкого динамического диапазона до 128 бит. Соответственно, параметр <math>n</math> варьировался от 3 до 43. Методы построения преобразователей были заимствованы из книги ''Residue number systems: Theory and implementation (Amos Omondi, Benjamin Premkumar)''. | ||
| − | == | + | == Генераторы Verilog-модулей == |
| + | Исследовались следующие преобразователи: | ||
| + | # [http://vscripts.ru/2012/forward-converter-2supn-generator.php Генератор Verilog для прямого преобразователя в базиса вида (2<sup>n</sup>-1, 2<sup>n</sup>, 2<sup>n</sup>+1)] - прямой преобразователь из позиционной системы счисления в систему остаточных классов (версия Романа). | ||
| + | # [http://vscripts.ru/dima/fwd_generator.php Генератор Verilog для прямого преобразователя в базиса вида (2<sup>n</sup>-1, 2<sup>n</sup>, 2<sup>n</sup>+1)] - прямой преобразователь из позиционной системы счисления в систему остаточных классов (версия Димы). | ||
| + | # [http://vscripts.ru/2012/reverse-converter-2supn-generator.php Генератор Verilog для обратного преобразователя из базиса вида (2<sup>n</sup>-1, 2<sup>n</sup>, 2<sup>n</sup>+1)] - сверхбыстрый обратный преобразователь в позиционную систему. | ||
Версия 08:00, 12 апреля 2013
Для того чтобы проанализировать конкурентоспособность модулярной арифметики, были проведены тесты прямых/обратных преобразователей для спец модулей вида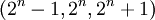 
. Сравнение производилось для широкого динамического диапазона до 128 бит. Соответственно, параметр 
варьировался от 3 до 43. Методы построения преобразователей были заимствованы из книги Residue number systems: Theory and implementation (Amos Omondi, Benjamin Premkumar).
Генераторы Verilog-модулей
Исследовались следующие преобразователи:
- Генератор Verilog для прямого преобразователя в базиса вида (2n-1, 2n, 2n+1) - прямой преобразователь из позиционной системы счисления в систему остаточных классов (версия Романа).
- Генератор Verilog для прямого преобразователя в базиса вида (2n-1, 2n, 2n+1) - прямой преобразователь из позиционной системы счисления в систему остаточных классов (версия Димы).
- Генератор Verilog для обратного преобразователя из базиса вида (2n-1, 2n, 2n+1) - сверхбыстрый обратный преобразователь в позиционную систему.
