Система остаточных классов - введение
Содержание
Теоретико-числовая база построения системы остаточных классов
Напомним определение деления с остатком.
Определение. Говорят, что целое число  делится на натуральное число
делится на натуральное число  с остатком, если имеется пара чисел
с остатком, если имеется пара чисел 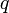 и
и  , где
, где 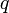 - целое,
- целое,  - натуральное или ноль, причём
- натуральное или ноль, причём 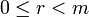 , такие, что
, такие, что 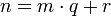 .
.
 называется делимым,
называется делимым,  - делителем,
- делителем, 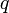 - неполным частным,
- неполным частным,  - остатком.
- остатком.
Пример: 48 при делении на 5 даёт остаток 3, т.к. 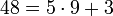 ,
, 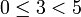 , -48 при делении на 5 даёт остаток 2, т.к.
, -48 при делении на 5 даёт остаток 2, т.к. 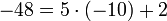 ,
, 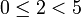 .
.
Сравнения и их основные свойства
Возьмём произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на
и будем рассматривать остатки при делении на  различных целых чисел.
различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Определение. Два целых числа  и
и  называются сравнимыми по модулю m, если их разность Невозможно разобрать выражение (лексическая ошибка): a − b
называются сравнимыми по модулю m, если их разность Невозможно разобрать выражение (лексическая ошибка): a − b
делится без остатка на.
Символически сравнимость записывается в виде формулы (сравнения):
Число  называется модулем сравнения.
называется модулем сравнения.
Эквивалентная формулировка:
Определение’. Целые числа  и
и  называются сравнимыми по модулю m, если остатки от деления этих чисел на
называются сравнимыми по модулю m, если остатки от деления этих чисел на равны.
равны.
Отношение сравнимости по модулю  обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
Отнесём все целые числа, дающие при делении на  один и тот же остаток в один класс, поэтому получится
один и тот же остаток в один класс, поэтому получится  различных классов по модулю
различных классов по модулю  .
Множество всех чисел сравнимых с
.
Множество всех чисел сравнимых с  по модулю
по модулю  называется классом вычетов
называется классом вычетов  по модулю
по модулю  .
.
Подробнее о свойствах сравнений и классах вычетов смотри Сравнения и их основные свойства