Сравнения и их основные свойства
Материал из Модулярная арифметики
Версия от 11:10, 25 августа 2014; Isaeva (обсуждение | вклад)
Возьмём произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на
и будем рассматривать остатки при делении на  различных целых чисел.
различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Определения
Примеры
Свойства
Для фиксированного натурального числа  отношение сравнимости по модулю
отношение сравнимости по модулю  обладает следующими свойствами:
обладает следующими свойствами:
- рефлексивности: для любого целого
 справедливо
справедливо 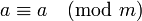 .
.
- симметричности: если
 , то
, то 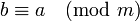 .
.
- транзитивности: если
 и
и 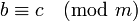 , то
, то 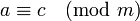 .
.
Таким образом, отношение сравнимости по модулю  является отношением эквивалентности на множестве целых чисел.
является отношением эквивалентности на множестве целых чисел.