Числа Мерсенна и Ферма

При рассмотрении отдельных классов простых чисел значительный интерес представляет вопрос о простых числах специального вида, например, числа Мерсенна или числа Ферма.

Определение

Числа Мерсенна — числа вида 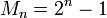$M_n = 2^n - 1$, где $n$ — натуральное число. Названы в честь французского математика Марена Мерсенна.

Иногда числами Мерсенна называют только числа 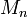$M_n$ с нечетными или простыми индексами n.

Множества простых чисел в этих последовательностях совпадают, а потому понятие простого числа Мерсенна не зависит от того, как именно определяются числа Мерсенна.

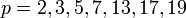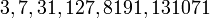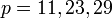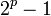При простых значениях n = p число может оказаться простым, но может быть составным. Например, при $p = 2, 3, 5, 7, 13, 17, 19$ мы получаем простые числа Мерсенна: $3, 7, 31, 127, 8191, 131071$, а при $p = 11, 23, 29$ числа $2^p - 1$ - составные.

Свойства чисел Мерсенна

• Если 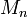$M_n$ является простым, то число n также простое. Обратное в общем случае неверно, наименьшим контрпримером является $M_{11} = 2047 = 23\cdot 89$.

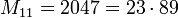• Любой делитель числа 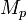$M_p$ для простого p имеет вид 2pk+1, где k — натуральное число (следствие малой теоремы Ферма).

Числа Мерсенна получили известность в связи с эффективным тестом простоты Люка — Лемера, благодаря которому простые числа Мерсенна давно удерживают лидерство как самые большие известные простые числа.

Определение

Числа Ферма — числа вида 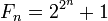$F_n=2^{2^n}+1$, где n — неотрицательное целое число.

При 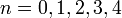$n = 0, 1, 2, 3, 4$ числа Ферма простые: $3, 5, 17, 257, 65537$.

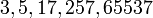Все числа Мерсенна и Ферма – взаимно простые.

Необходимо отметить, что значения чисел Мерсенна и Ферма быстро растут. Это не позволяет использовать лишь их в качестве модуле СОК.

Операции над числами Мерсенна и Ферма