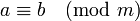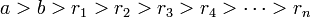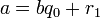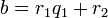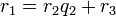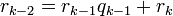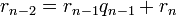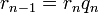Система остаточных классов - введение
Содержание
Теоретико-числовая база построения системы остаточных классов
Напомним определение деления с остатком.
Определение
Говорят, что целое число 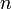 делится на натуральное число
делится на натуральное число  с остатком, если имеется пара целых чисел
с остатком, если имеется пара целых чисел 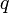 и
и  , таких, что
, таких, что 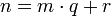 и
и 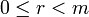 .
.
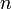 называется делимым,
называется делимым,  - делителем,
- делителем, 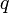 - неполным частным,
- неполным частным,  - остатком.
- остатком.
Для целых чисел:
Определение
Говорят, что целое число 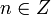 делится на натуральное число
делится на натуральное число 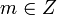 с остатком, если имеется пара целых чисел
с остатком, если имеется пара целых чисел 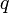 и
и  , таких, что
, таких, что 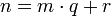 и
и 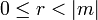 .
.
Пример:
48 при делении на 5 даёт остаток 3, т.к. 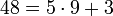 ,
, 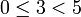 , -48 при делении на 5 даёт остаток 2, т.к.
, -48 при делении на 5 даёт остаток 2, т.к. 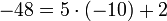 ,
, 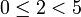 .
.
Сравнения и их основные свойства
Возьмём произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на
и будем рассматривать остатки при делении на  различных целых чисел.
различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Определение
Два целых числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если их разность
, если их разность 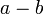 делится без остатка на
делится без остатка на  .
.
Символически сравнимость записывается в виде формулы (сравнения):
Число  называется модулем сравнения.
называется модулем сравнения.
Эквивалентная формулировка:
Определение
Целые числа  и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если остатки от деления этих чисел на
, если остатки от деления этих чисел на  равны.
равны.
Отношение сравнимости по модулю  обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности.
Отнесём все целые числа, дающие при делении на  один и тот же остаток в один класс, поэтому получится
один и тот же остаток в один класс, поэтому получится  различных классов по модулю
различных классов по модулю  .
Множество всех чисел сравнимых с
.
Множество всех чисел сравнимых с  по модулю
по модулю  называется классом вычетов
называется классом вычетов  по модулю
по модулю  .
.
Подробнее о свойствах сравнений и классах вычетов смотри Сравнения и их основные свойства
Теорема о делении с остатком. Алгоритм Евклида
Теорема о делении с остатком
Для любых целых a и b, 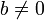 , существует единственный набор целых чисел q и r, что a = bq + r и
, существует единственный набор целых чисел q и r, что a = bq + r и 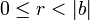 , где |b| — модуль числа b.
, где |b| — модуль числа b.
На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.
Алгоритм Евклида для целых чисел
Пусть  и
и  — целые числа, не равные одновременно нулю, и последовательность чисел
— целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое 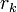 — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
— это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
Тогда НОД(a,b), наибольший общий делитель  и
и  , равен
, равен
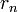 , последнему ненулевому члену этой последовательности.
, последнему ненулевому члену этой последовательности.
Существование таких 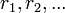 , то есть возможность деления с остатком
, то есть возможность деления с остатком  на
на  для любого целого
для любого целого  и целого
и целого 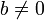 , доказывается индукцией.
, доказывается индукцией.
Корректность этого алгоритма вытекает из следующих двух утверждений:
- Пусть
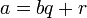 , тогда НОД (
, тогда НОД ( ,
,  ) = НОД (
) = НОД ( ,
,  ).
).
- НОД(0,
 ) =
) =  для любого ненулевого
для любого ненулевого  (так как 0 делится на любое целое число, кроме нуля).
(так как 0 делится на любое целое число, кроме нуля).
Китайская теорема об остатках
Фундаментальным положением, лежащим в основе модулярного представления чисел, является китайская теорема об остатках (Chinese Remainder Theorem - CRT). Например, эта теорема гарантирует, что при правильном выборе модулей СОК каждое число из динамического диапазона имеет в СОК единственное представление, и по этому представлению можно определить представленное число. В своей первоначальной формулировке эта теорема была доказана китайским математиком Сунь-Цзы приблизительно в 100 г. н.э. В современной формулировке теорема звучит так:
Теорема
Пусть 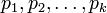 - попарно взаимно простые числа, большие 1, и пусть
- попарно взаимно простые числа, большие 1, и пусть 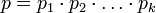 . Тогда существует единственное неотрицательное решение по модулю
. Тогда существует единственное неотрицательное решение по модулю  следующей системы сравнений:
следующей системы сравнений:
-
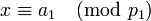 ,
,
-
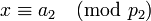 ,
,
-
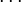 ,
,
-
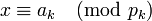 .
.
Другими словами, отображение, которое каждому целому числу 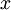 ,
, 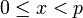 , ставит в соответствие кортеж
, ставит в соответствие кортеж 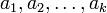 , где
, где 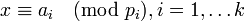 является биекцией кольца
является биекцией кольца 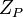 на декартово произведение
на декартово произведение 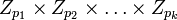 колец
колец 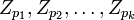 .
.
Подробности и доказательство теоремы смотри Китайская теорема об остатках.
Смотри также Китайская теорема об остатках(КТО II), Китайская теорема об остатках (КТО III).
Теоремы Эйлера и Ферма, их роль в вычислении мультипликативных обратных элементов по заданному модулю
Определение
Функция Эйлера 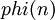 — это количество чисел от
— это количество чисел от 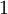 до
до 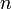 , взаимно простых с
, взаимно простых с 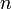 .
.
Т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с 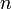 равен единице.
равен единице.
Tеоремa Эйлера
Если  и
и  взаимно просты, то
взаимно просты, то 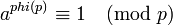 , где
, где 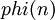 - функция Эйлера.
- функция Эйлера.
В частном случае, когда  простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Частным случаем теоремы Эйлера является малая теорема Ферма.
простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Частным случаем теоремы Эйлера является малая теорема Ферма.
Малая теорема Ферма
Если  - простое число и
- простое число и  - произвольное целое число, не делящееся на
- произвольное целое число, не делящееся на  , то
, то 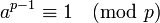 .
.
Смотри Функция Эйлера, Вычисление мультипликативных обратных элементов по заданному модулю.
Числа Мерсенна, Ферма и операции над ними
При рассмотрении отдельных классов простых чисел интерес представляет вопрос о простых числах специального вида, например, числа Мерсенна или числа Ферма.
Определение
Числа Мерсенна — числа вида 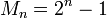 , где
, где 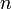 — натуральное число.
Названы в честь французского математика Марена Мерсенна.
— натуральное число.
Названы в честь французского математика Марена Мерсенна.
Иногда числами Мерсенна называют только числа 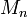 с нечетными или простыми индексами n.
с нечетными или простыми индексами n.
Множества простых чисел в этих последовательностях совпадают, а потому понятие простого числа Мерсенна не зависит от того, как именно определяются числа Мерсенна.
При простых значениях n = p число может оказаться простым, но может быть составным.
Например, при 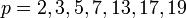 мы получаем простые числа Мерсенна:
мы получаем простые числа Мерсенна: 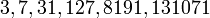 , а при
, а при 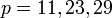 числа
числа 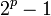 - составные.
- составные.
Определение
Числа Ферма — числа вида 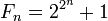 , где n — неотрицательное целое число.
, где n — неотрицательное целое число.
При 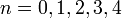 числа Ферма простые:
числа Ферма простые: 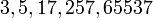 . Известно, что для
. Известно, что для 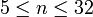 числа
числа 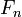 являются составными. На 2014 г. не найдено ни одного простого числа такого вида для
являются составными. На 2014 г. не найдено ни одного простого числа такого вида для 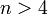 .
.
Все числа Мерсенна и Ферма – взаимно простые. Кроме того, для модулей СОК вида 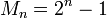 ,
, 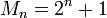 легко реализуется преобразование и арифметические операции. Поэтому эффективно выбирать модули СОК в виде чисел Мерсенна и Ферма.
легко реализуется преобразование и арифметические операции. Поэтому эффективно выбирать модули СОК в виде чисел Мерсенна и Ферма.
Смотри Числа Мерсенна и Ферма.
Математические модели модулярного представления и параллельной обработки информации
Представление числа в системе остаточных классов. Модульные операции
Основные методы и алгоритмы перехода от позиционного представления к остаткам
Восстановление позиционного представления числа по его остаткам
Система остаточных классов обладает одной особенностью, которую можно отнести к недостаткам этой системы: нельзя визуально определить величину числа, представленного в СОК, а следовательно затруднительно и выполнение таких операций, как сравнение чисел, определение знака числа. Один из путей решения этой проблемы состоит в преобразовании чисел из СОК в позиционную систему счисления. Оценим существующие способы перевода, как традиционные: метод ортогональных базисов; перевод числа в обобщенную позиционную систему (ОПС), так и недавно появившиеся интервальные методы перевода.
Метод ортогональных базисов
Метод восстановления числа по его остаткам был найден еще в Китае две тысячи лет назад. Основой этого метода является теорема, названная Китайской теоремой об остатках (КТО).
Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления.
Смотри Метод ортогональных базисов.
Перевод числа из СОК в обобщенную позиционную систему (ОПС)
Еще один метод определения величины числа связан с переводом числа из системы остаточных классов в ОПС. Для того, чтобы рассмотреть этот метод, выявим связь между представлением некоторого числа в этих двух системах.
Пусть по-прежнему СОК задается основаниями число в этой системе. И пусть – также основания ОПС, тогда число можно представить в виде
где – коэффициенты (цифры) ОПС.
Очевидно, что диапазоны чисел, представимых в СОК и ОПС совпадают, т.е. можно говорить о наличии взаимно однозначного соответствия между множеством представлений чисел в СОК и ОПС.
Это равенство можно переписать в следующем виде:
откуда следует, что цифры ОПС могут быть получены из соотношений:
Причем при определении цифр по формулам все вычисления можно вести в СОК.
Смотри Перевод числа из СОК в обобщенную позиционную систему.
Интервальные методы перевода
Достаточно эффективными методами перевода чисел из СОК в ПСС являются интервальные методы, основанные на интервальных характеристиках чисел. Одна из таких характеристик – номер интервала.
Смотри Интервальные методы перевода.
Расширение диапазона представления чисел
Расширение системы оснований является одной из основных немодульных операций в СОК. Выполнение этой операции бывает необходимо при выполнении операции деления чисел, при вычислении позиционных характеристик, при обнаружении переполнения при выполнении сложения или умножения чисел.
Задачу расширения системы оснований можно сформулировать следующим образом: найти остаточное представление числа по новому основанию (новым основаниям), если известно представление числа по другим основаниям остатки от деления на другие числа. Один из путей расширения системы оснований состоит в переводе числа в позиционную систему счисления и вычисления остатка от деления на новый модуль. Этот путь не является рациональным с точки зрения числа операций.
Другой метод расширения системы оснований позволяет определить цифру числа по новому основанию, базируясь на таких позиционных характеристиках числа, как ранг числа, след числа.
Смотри Расширение диапазона представления чисел.