Комплексное исследование умножителей в диапазоне 3 - 64 бит
В рамках работы по разработке эффективных модулярных устройств было проведено исследование различных вариантов построения однотактовых двоичных и модулярных умножителей с входными операндами в диапазоне 3-64 бит. Такие устройства чрезвычайно важны в современной микроэлектронике. Каждый современный микропроцессор имеет такую операцию в составе своего набора инструкций, а продвинутые DSP процессоры содержат специальные вычислительные блоки для ускоренного вычисления [1]. Исследовались 4 варианта однотактовых умножителей:
- Встроенный умножитель в САПР Synopsys Design Compiler.
- Иерархический двоичный умножитель [1].
- Модулярный умножитель со стандартным спец. базисом из трех модулей (3 moduli set)
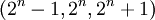
- Модулярный умножитель с продвинутым спец. базисом из 4-х модулей (4 moduli set)
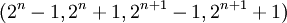
Синтез проводился в базисе 45 нм. в библиотеке NangateOpenCellLibrary.lib с помощью САПР Synopsys Design Compiler. Синтез проводился дважды для каждой из схем, на разных настройках "усилий" синтезатора - medium и ultra high effort. Таким образом, также проверялась способность САПРа по минимизации задержек для различных схем. Общее количество тестов выглядит следующим образом.
| Модулярный | Двоичный | ||||||
| 3 moduli set | 4 moduli set | Встроенный | Иерархический | ||||
| medium effort | ultra effort | medium effort | ultra effort | medium effort | ultra effort | medium effort | ultra effort |
Содержание
Ссылки на генераторы Verilog описаний исследуемых схем
Для каждой из схем были написаны генераторы поведенческих описаний на языке Verilog:
- Модулярный умножитель со стандартным спец. базисом из трех модулей (3 moduli set)
- Модулярный умножитель с продвинутым спец. базисом из 4-х модулей (4 moduli set)
- Иерархический двоичный умножитель
- Встроенный умножитель в САПР Synopsys Design Compiler.
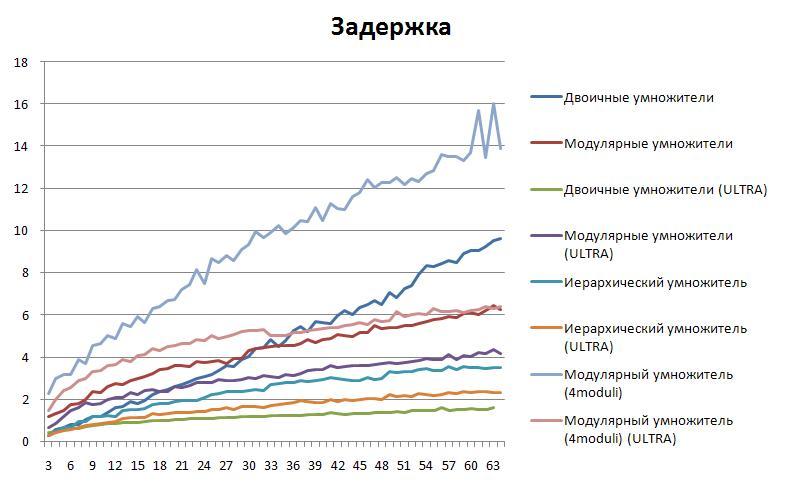
Общие результаты
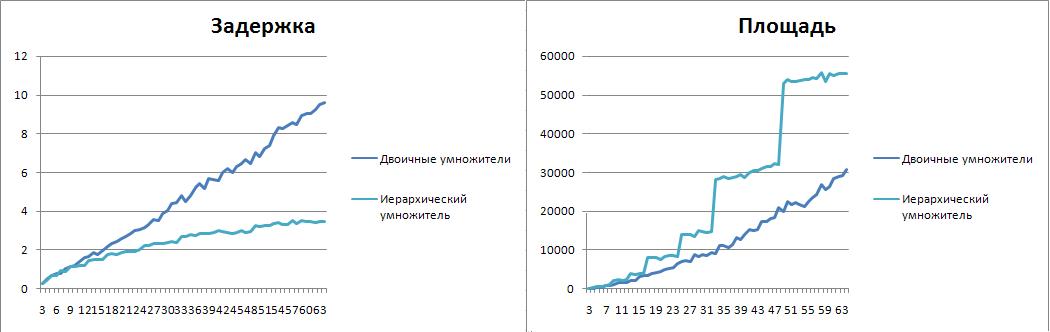
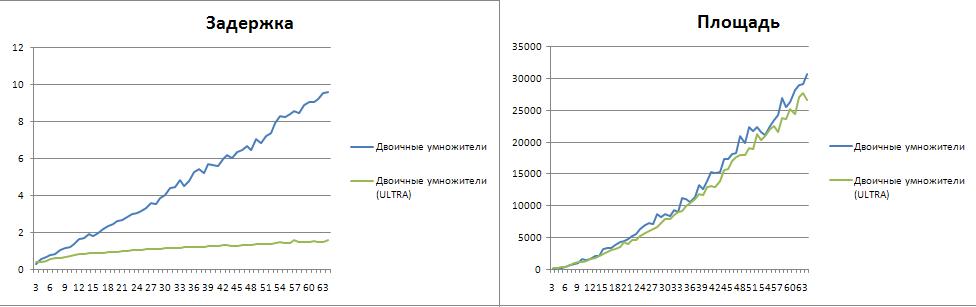
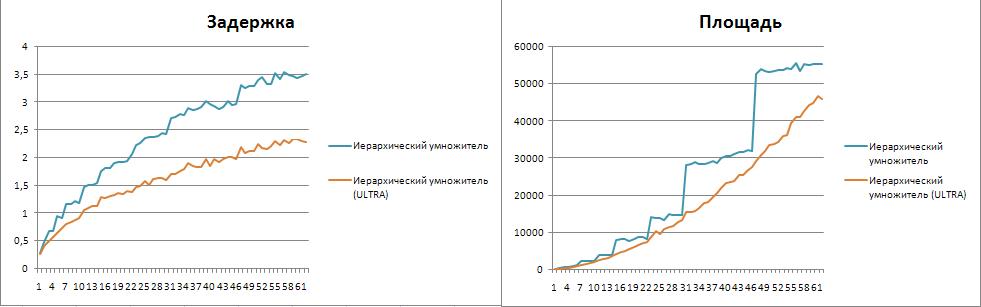
Сравнение двоичных схем
Иерархический умножитель прекрасно себя показал в сравнении с встроенным вариантом. Несмотря на возрастающую площадь, задержка сократилась примерно вдвое. Однако, на ULTRA настройках синтезатора все преимущества сошли на нет. И в площади и в задержке встроенный вариант "Synopsys DC" значительно превзошел иерархическую схему. Встроенный вариант оказался наиболее "восприимчив" к настройкам синтезатора.
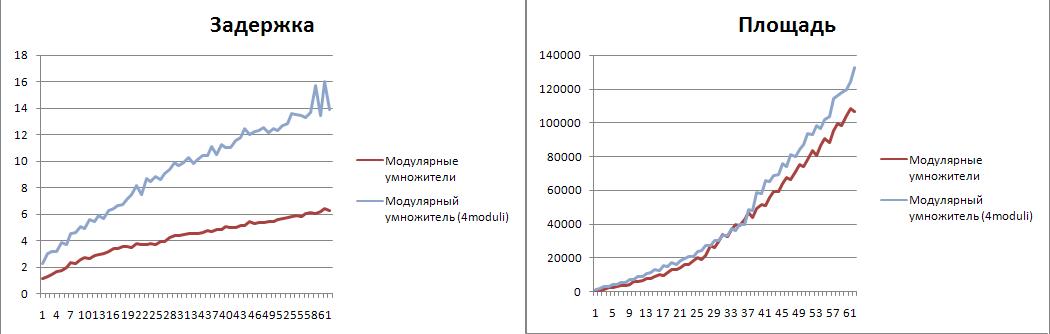
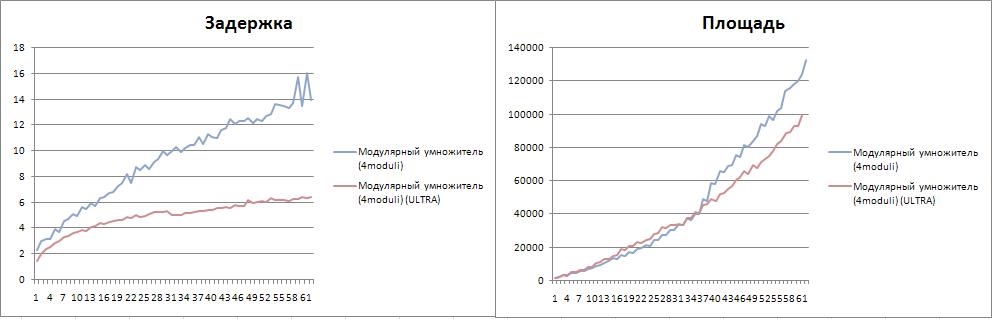
Сравнение модулярных схем
Модулярная структура, основанная на 3-х основаниях 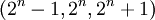 показала себя намного лучше, чем предлагаемая в
[2] структура с 4-мя основаниями
показала себя намного лучше, чем предлагаемая в
[2] структура с 4-мя основаниями 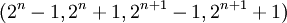 . Задержка на критическом пути для 4-модульного набора больше в два раза. Возможно, причиной тому послужила недостаточно эффективная реализация преобразователей. Так же есть вероятность, что такая структура будет более эффективна для больших задач с значительным количеством арифметических операций. Эти предположения требуют дальнейших исследований.
. Задержка на критическом пути для 4-модульного набора больше в два раза. Возможно, причиной тому послужила недостаточно эффективная реализация преобразователей. Так же есть вероятность, что такая структура будет более эффективна для больших задач с значительным количеством арифметических операций. Эти предположения требуют дальнейших исследований.
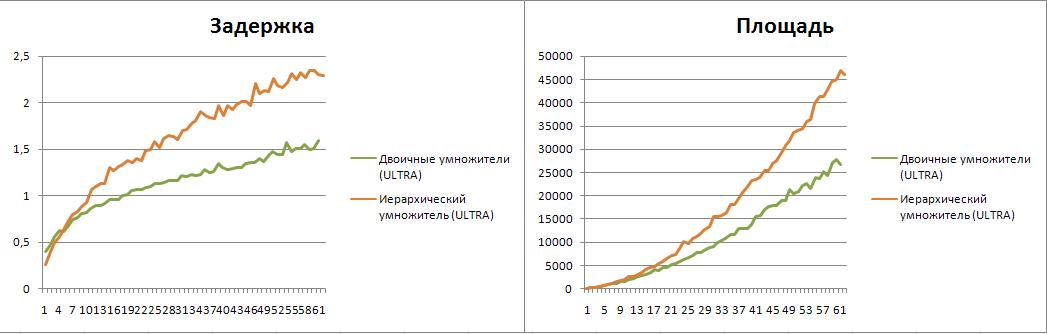
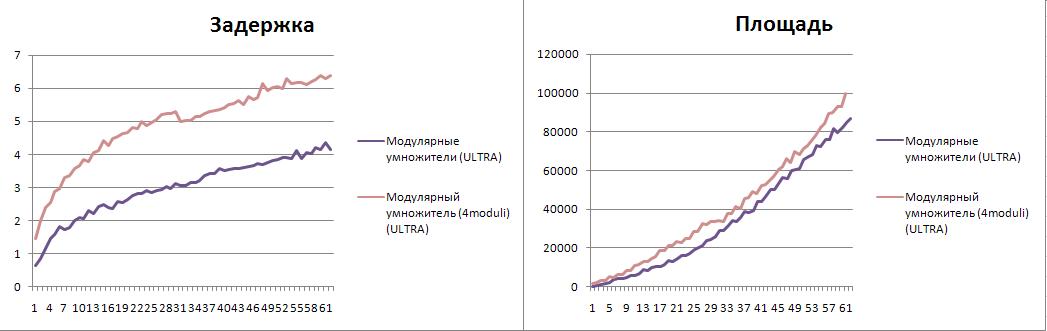
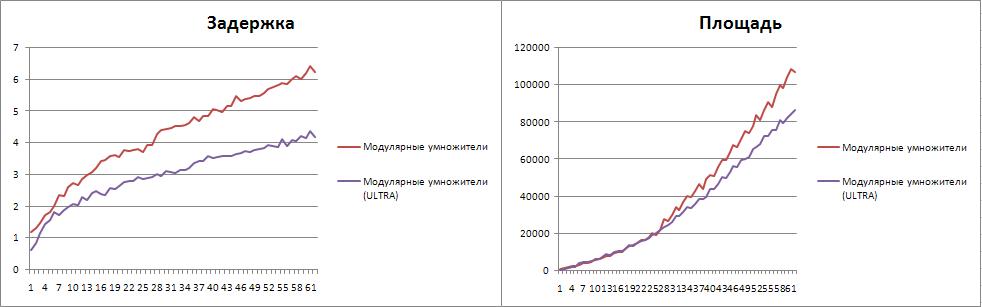
Анализ эффективности САПР в режиме ULTRA high effort
Графики скомпонованы для иллюстрации эффективности ULTRA режима.
Наибольшую эффективность режима удалось достичь на схеме встроенного умножителя. Наименьшее влияние режим оказал на модулярные схемы. Средние значения коэффициентов увеличения производительности сведены в табличку.
| Схема умножителя | Средний коэффициент увеличения производительности |
| Встроенный умножитель в САПР Synopsys Design Compiler. | 68 |
| Иерархический двоичный умножитель | 31 |
| Модулярный умножитель со стандартным спец. базисом из трех модулей | 28 |
| Модулярный умножитель с продвинутым спец. базисом из 4-х модулей | 38 |
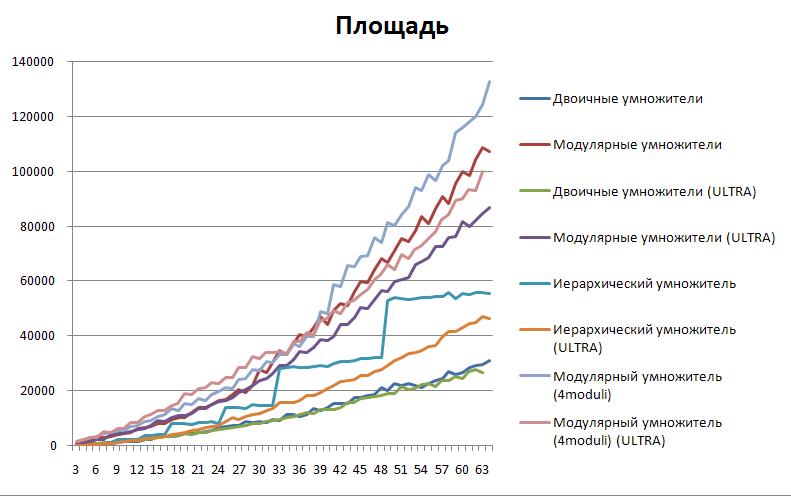
Площадь также сокращается. Наибольшее сокращение продемонстрировал иерархический умножитель.
Выводы
Наилучшими результатами в стандартном режиме обладают иерархические сумматоры. В режиме ULTRA high effort, наилучшими показателями обладает обычный встроенный умножитель. Наихудшие показатели оказались у 4-х модульного набора. Вероятно, это связанно с недостаточной оптимизацией и в дальнейшем удастся исправить ситуацию. Трехмодульный набор неплохо показал себя в сравнении с встроенным вариантом в стандартном режиме, после 32 бит выигрывая в производительности. Однако, иерархический подход не оставил шансов. А в ULTRA effort и вовсе все двоичные схемы оказались в преимуществе. Таким образом, модулярная арифметика вновь проигрывает двоичной.
UPDATE 07.06.13
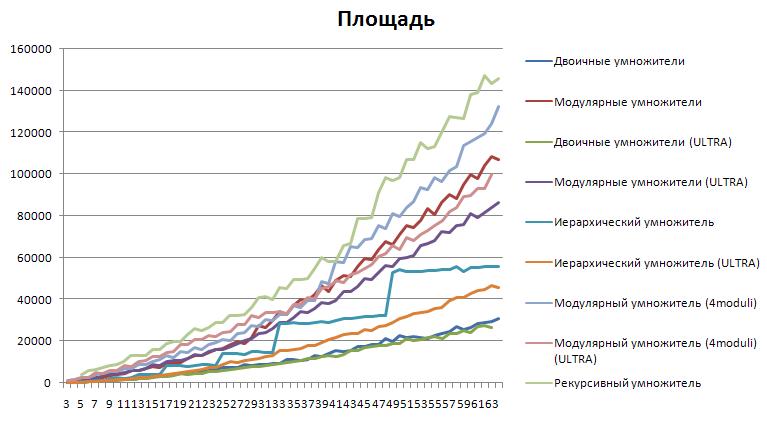
Добавлены результаты тестов рекурсивного умножителя.
Можно видеть, что рекурсивный вариант является "чемпионом" по занимаемой площади схем. А по временным характеристикам - на втором месте с конца. В плане задержки хуже рекурсивного - только 4-х модульный базис. Хотя, если приглядеться, то можно видеть что рекурсивный умножитель после 58-го бита начинает выигрывать у двоичного. Это в принципе согласуется с идеей того что рекурсивная арифметика начинает выигрывать на еще более масштабных задачах, нежли традиционная модулярная арифметика.
Используемая литература
[1] Vladimir V.Erokhin "Integer multiplication algorithms. Methodology and implementation results"